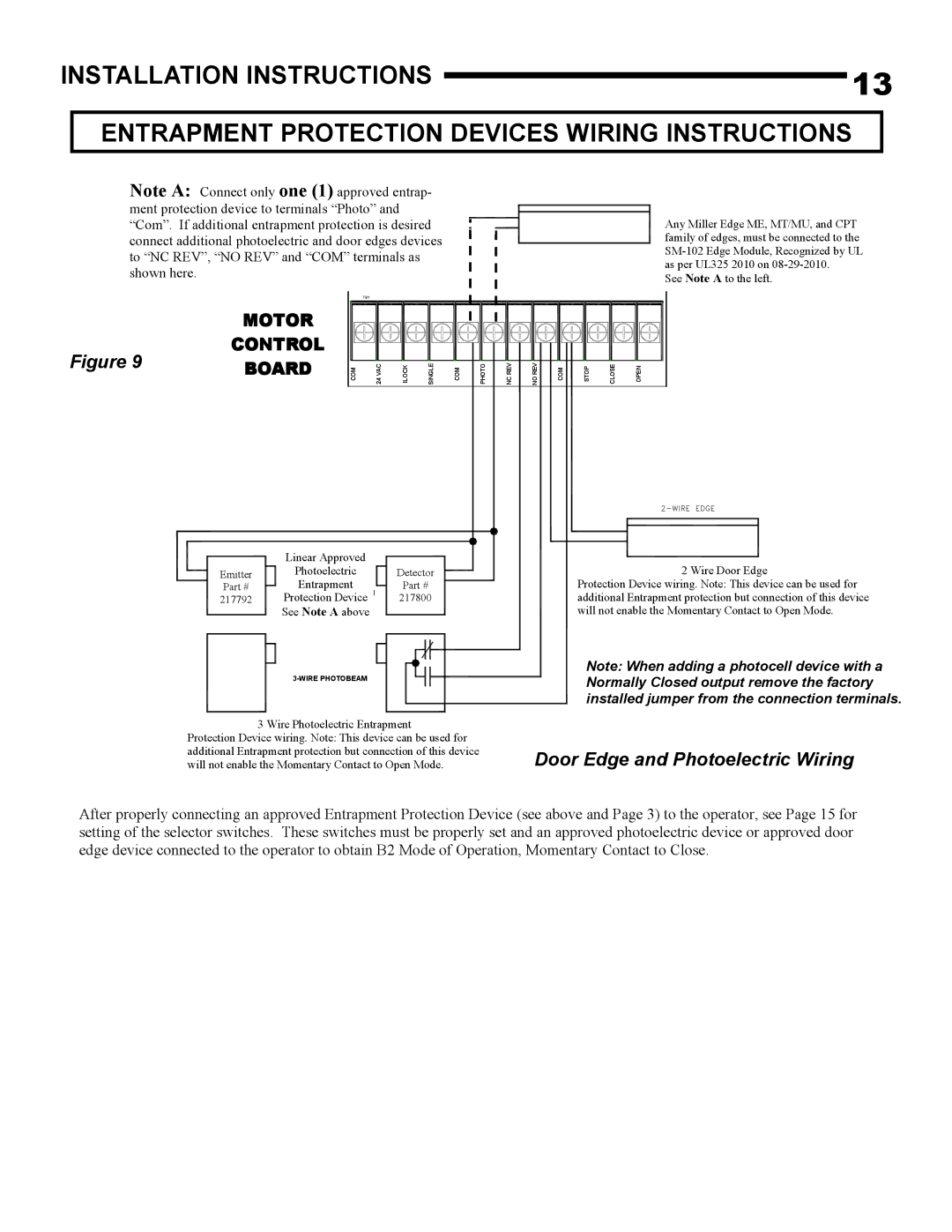
H-S, J-S specifications
Linear J-S and H-S are two prominent approaches in the realm of signal processing, particularly focusing on data compression and transmission efficiency. They provide robust methodologies for managing data in systems where bandwidth and storage are critical factors.Linear J-S, or Linear Jordan-Space signal processing, is characterized by its ability to utilize linear transformations to represent signal variations with minimal loss of information. The main feature of this approach lies in its capacity to maintain high fidelity in signals while significantly reducing bandwidth consumption. By employing linear transformations, such as Fourier or wavelet transforms, Linear J-S efficiently captures the essential components of a signal. This methodology is particularly useful in scenarios involving audio and video data, where maintaining quality during compression is paramount.
One significant technology underpinning Linear J-S is the Fast Fourier Transform (FFT), which allows for rapid computation of the frequency components of a signal. This enables real-time processing and enhances the performance of systems that rely on rapid data transmission. Another critical aspect of Linear J-S is its adaptability to various data types, making it suitable for applications in telecommunications, multimedia, and even biomedical engineering.
On the other hand, Linear H-S, or Linear Harmonic-Skew signal processing, takes a different approach by focusing on harmonic analysis. This technique examines the harmonic content of signals to develop models that can accurately reconstruct the original data from its compressed form. The primary feature of Linear H-S is its robust handling of periodic signals, which allows for accurate representation even in the presence of noise.
Linear H-S technologies often leverage Adaptive Filter Theory and the Discrete Cosine Transform (DCT), which are effective in minimizing artifacts and preserving the integrity of the signal. This makes Linear H-S highly applicable in areas like image processing, where it plays a critical role in JPEG compression, ensuring that the visual quality remains intact without unnecessarily large file sizes.
Both Linear J-S and H-S employ algorithms designed for optimal reconstruction of signals from their compressed forms, emphasizing the need for low latency in applications where speed is crucial. They each have their unique characteristics, making them suitable for different types of signals and applications. While Linear J-S excels in the realm of audio and complex data types, Linear H-S proves to be invaluable in scenarios involving repetitive patterns and periodic signals.
In conclusion, Linear J-S and H-S represent two sophisticated methodologies in signal processing, each with distinct features and technologies designed to optimize data compression while faithfully preserving signal quality. Their applications span across various industries, showcasing their importance in contemporary data communication and multimedia systems.