HP 33s Scientific manual Normal and Inverse-Normal Distributions, Logarithmic Exponential Power

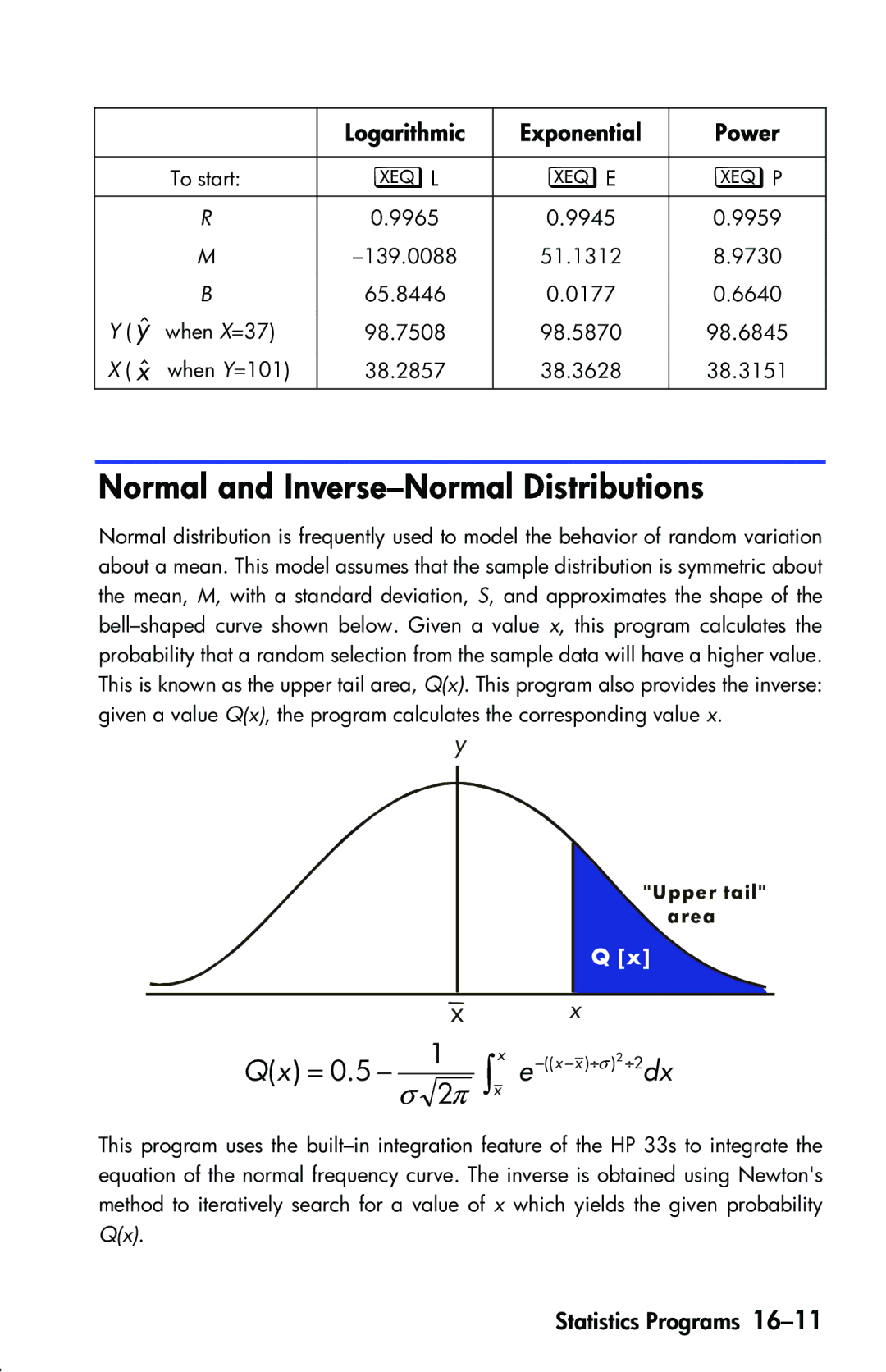
	Logarithmic	Exponential	Power
To start:	XL	XE	XP
R	0.9965	0.9945	0.9959
M	–139.0088	51.1312	8.9730
B	65.8446	0.0177	0.6640
Y ( yˆ when X=37)	98.7508	98.5870	98.6845
X ( xˆ when Y=101)	38.2857	38.3628	38.3151

Normal and Inverse–Normal Distributions

Normal distribution is frequently used to model the behavior of random variation about a mean. This model assumes that the sample distribution is symmetric about the mean, M, with a standard deviation, S, and approximates the shape of the bell–shaped curve shown below. Given a value x, this program calculates the probability that a random selection from the sample data will have a higher value. This is known as the upper tail area, Q(x). This program also provides the inverse: given a value Q(x), the program calculates the corresponding value x.

y

"Upper tail" area

Q [x]

x x

Q(x) = 0.5 − σ 12π ≥xx e −((x −x )⎟σ )2 ⎟2dx

This program uses the built–in integration feature of the HP 33s to integrate the equation of the normal frequency curve. The inverse is obtained using Newton's method to iteratively search for a value of x which yields the given probability Q(x).

Statistics Programs 16–11