Fairchild AN-7502 manual Characterization-Curve Limits, Conclusions, Application Note

Application Note 7502

For peak gate voltages other than 10 volts, and load resis-

tances other than BVDSS/ID(MAX), the equations of Table 1 may be used in conjunction with slope estimates from the

characterization curves for CX and CGS + CX(1 + gM/gMJ) at the appropriate drain-current level.

Characterization-Curve Limits

The switching-time range over which the characterization can be applied is very impressive. For gate currents of the order of microamperes, device dissipation is the limiting factor. For gate currents of the order of amperes, the device response will be slowed by gate propagation delay. This delay, of course, degrades the linear switching relationship to gate current. How- ever, as Figure 12 graphically shows, the characterization is valid across five decades of gate current and switching time, allowing all but a very few switching applications to be described by the characterization curves of Figure 9.

	104
						RFM15N15
						tD(OFF)
	103					tR
						tF
						tD(ON)
- MICROSECONDS	102
	101
TIME(t)	100
	10-1
	10-2
	100	101	102	103	104	105	106

GATE CURRENT (IG) - MICROAMPERES

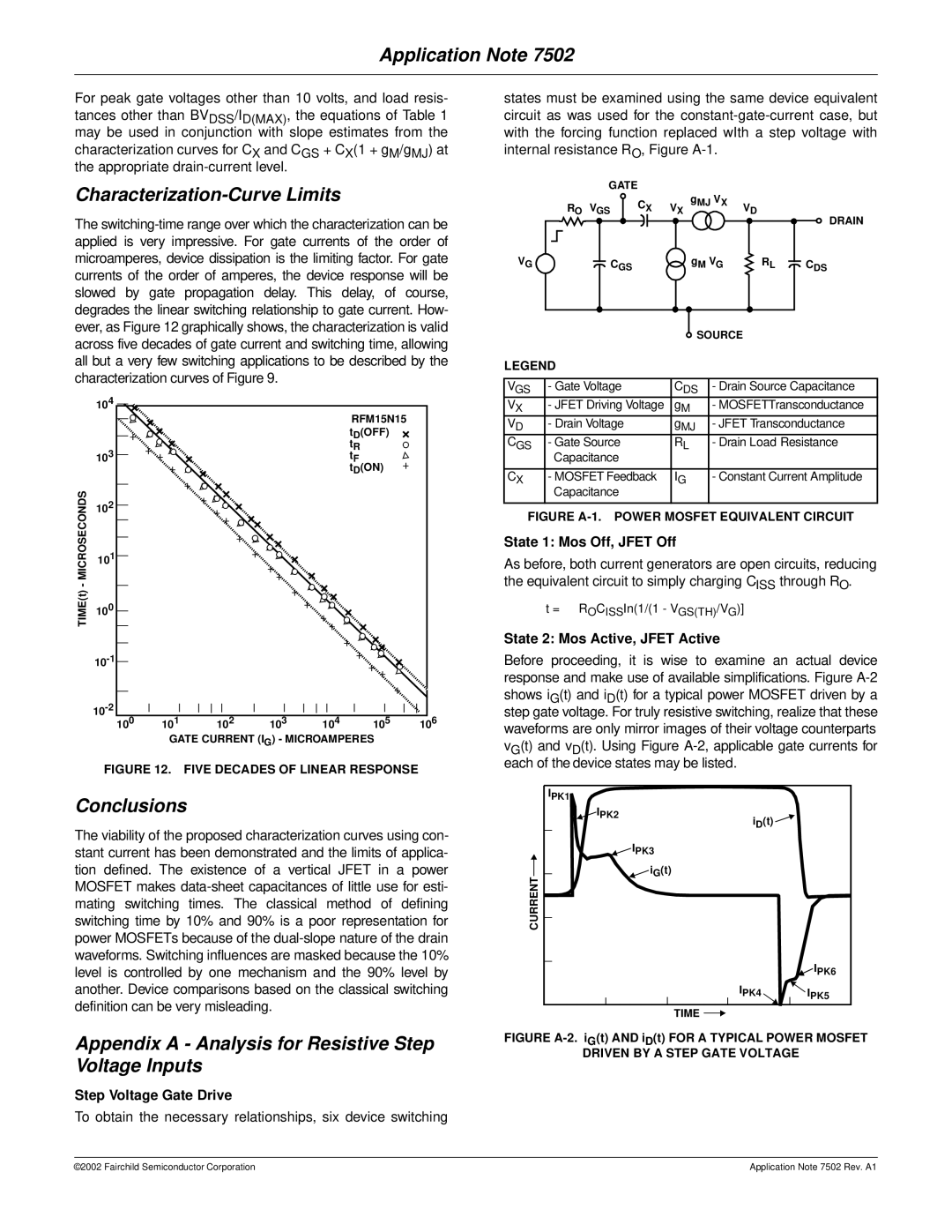
FIGURE 12. FIVE DECADES OF LINEAR RESPONSE

Conclusions

The viability of the proposed characterization curves using con- stant current has been demonstrated and the limits of applica- tion defined. The existence of a vertical JFET in a power MOSFET makes data-sheet capacitances of little use for esti- mating switching times. The classical method of defining switching time by 10% and 90% is a poor representation for power MOSFETs because of the dual-slope nature of the drain waveforms. Switching influences are masked because the 10% level is controlled by one mechanism and the 90% level by another. Device comparisons based on the classical switching definition can be very misleading.

Appendix A - Analysis for Resistive Step Voltage Inputs

Step Voltage Gate Drive

To obtain the necessary relationships, six device switching

states must be examined using the same device equivalent circuit as was used for the constant-gate-current case, but with the forcing function replaced wIth a step voltage with internal resistance RO, Figure A-1.

	GATE
R	V	CX	V	gMJ VX	V	D
O	GS			X			DRAIN
VG	CGS			gM VG		RL	CDS

SOURCE

LEGEND

VGS	- Gate Voltage	CDS	- Drain Source Capacitance
VX	- JFET Driving Voltage	gM	- MOSFETTransconductance
VD	- Drain Voltage	gMJ	- JFET Transconductance
CGS	- Gate Source	RL	- Drain Load Resistance
	Capacitance
CX	- MOSFET Feedback	IG	- Constant Current Amplitude
	Capacitance

FIGURE A-1. POWER MOSFET EQUIVALENT CIRCUIT

State 1: Mos Off, JFET Off

As before, both current generators are open circuits, reducing the equivalent circuit to simply charging CISS through RO.

t = ROCISSIn(1/(1 - VGS(TH)/VG)]

State 2: Mos Active, JFET Active

Before proceeding, it is wise to examine an actual device response and make use of available simplifications. Figure A-2 shows iG(t) and iD(t) for a typical power MOSFET driven by a step gate voltage. For truly resistive switching, realize that these waveforms are only mirror images of their voltage counterparts vG(t) and vD(t). Using Figure A-2, applicable gate currents for each of the device states may be listed.

IPK1
IPK2	iD(t)
	IPK3
CURRENT	iG(t)
		IPK6
	IPK4	I
		PK5

TIME

FIGURE A-2. iG(t) AND iD(t) FOR A TYPICAL POWER MOSFET

DRIVEN BY A STEP GATE VOLTAGE

©2002 Fairchild Semiconductor Corporation Application Note 7502 Rev. A1