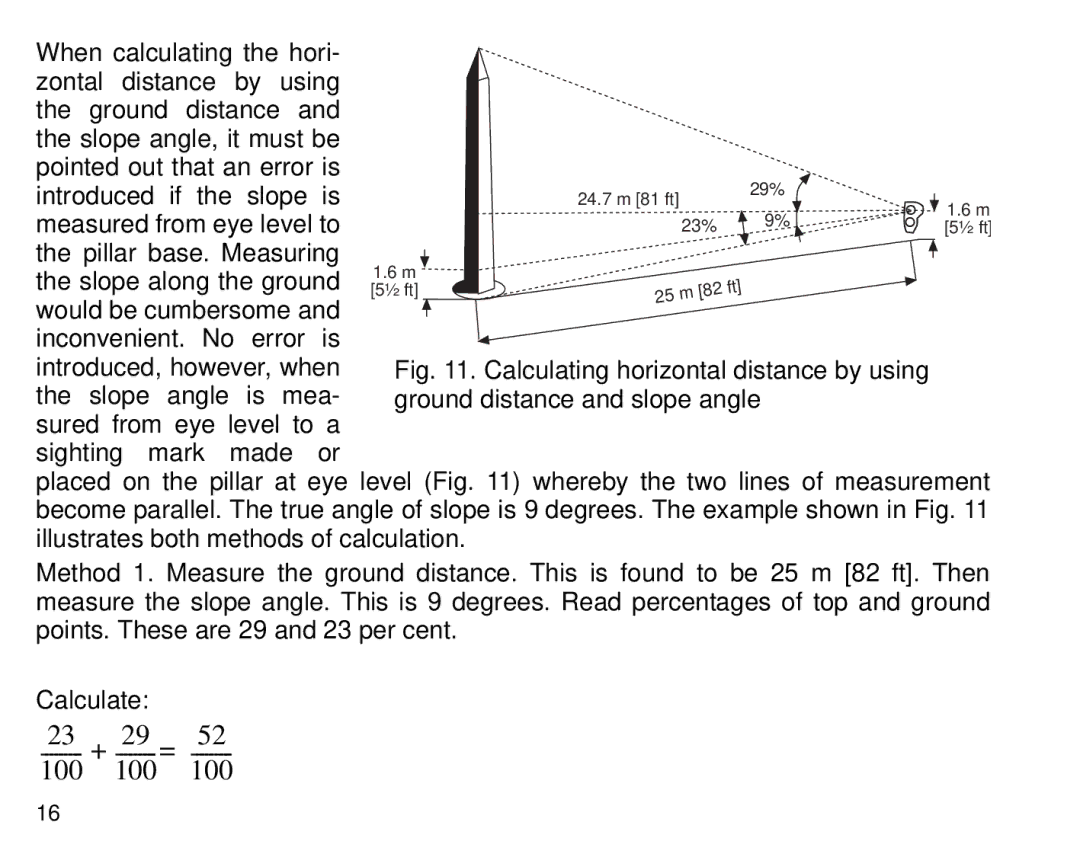
When calculating the hori- |
|
|
| |||
zontal distance | by using |
|
|
| ||
the ground distance and |
|
|
| |||
the slope angle, it must be |
|
|
| |||
pointed out that an error is |
| 29% |
| |||
introduced if the slope | is | 24.7 m [81 ft] | 1.6 m | |||
measured from eye level to | 23% | 9% | ||||
[5½ ft] | ||||||
the pillar base. Measuring | 1.6 m |
|
| |||
the slope along the ground |
|
| ||||
[5½ ft] |
|
| ||||
would be cumbersome and |
|
|
| |||
inconvenient. No error | is |
|
|
| ||
introduced, however, when | Fig. 11. Calculating horizontal distance by using |
| ||||
the slope angle is mea- | ground distance and slope angle |
| ||||
sured from eye level to a |
|
|
| |||
sighting mark | made | or |
|
|
| |
placed on the pillar at eye level (Fig. 11) whereby the two lines of measurement become parallel. The true angle of slope is 9 degrees. The example shown in Fig. 11 illustrates both methods of calculation.
Method 1. Measure the ground distance. This is found to be 25 m [82 ft]. Then measure the slope angle. This is 9 degrees. Read percentages of top and ground points. These are 29 and 23 per cent.
Calculate: |
| |
23 | 29 | 52 |
+ | ||
100 | 100 | 100 |
16