Suunto Tandem manual Lectura de la cúspide y la

Si la base de la columna se
encuentra		por encima	del
nivel de los ojos, la lectura
de	la base se resta de la			12.5 m
lectura de la cúspide y la				[33½ ft]
altura total es la diferencia
de	porcentajes de		la
distancia		horizontal.	Por
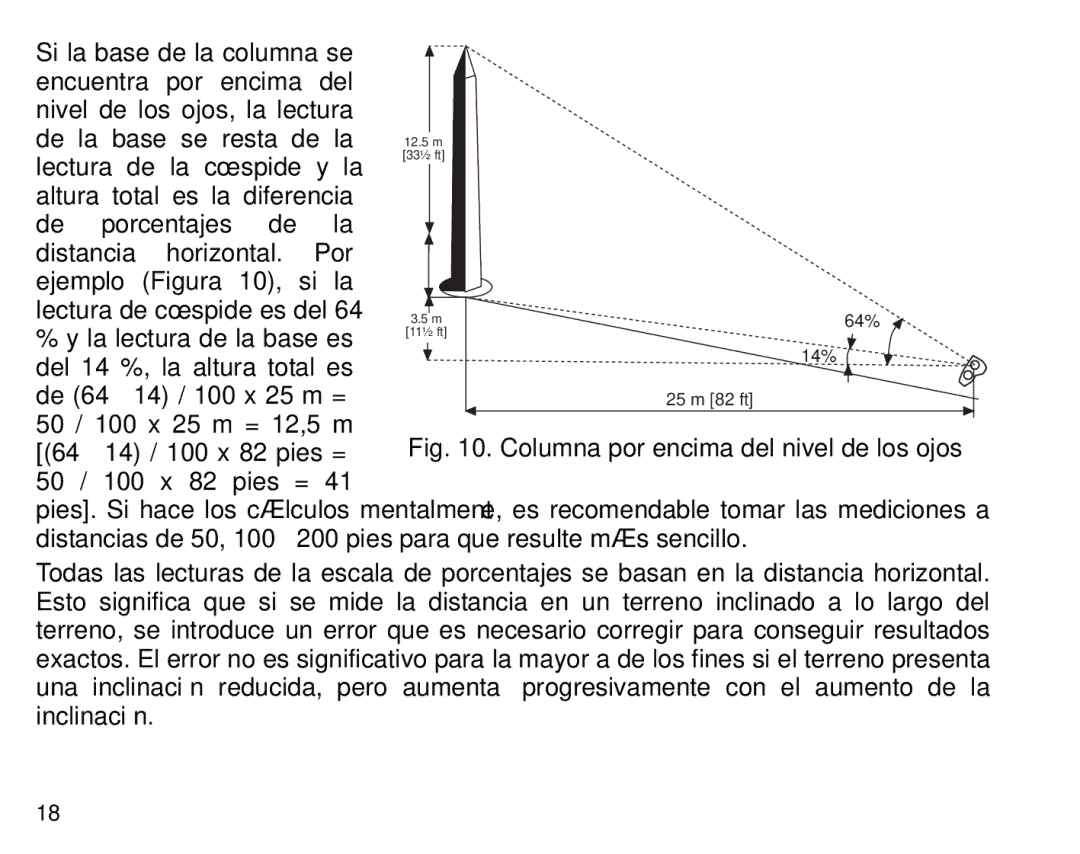
ejemplo (Figura 10), si la
lectura de cúspide es del 64				3.5 m	64%
% y la lectura de la base es				[11½ ft]
					14%
del 14 %, la altura total es
de (64 – 14) / 100 x 25 m =						25 m [82 ft]
50 / 100 x 25 m = 12,5 m				Fig. 10. Columna por encima del nivel de los ojos
[(64 – 14) / 100 x 82 pies =

50 / 100 x 82 pies = 41

pies]. Si hace los cálculos mentalmente, es recomendable tomar las mediciones a distancias de 50, 100 ó 200 pies para que resulte más sencillo.

Todas las lecturas de la escala de porcentajes se basan en la distancia horizontal. Esto significa que si se mide la distancia en un terreno inclinado a lo largo del terreno, se introduce un error que es necesario corregir para conseguir resultados exactos. El error no es significativo para la mayoría de los fines si el terreno presenta una inclinación reducida, pero aumenta progresivamente con el aumento de la inclinación.

18