Philips Semiconductors
Magnetoresistive sensors for
magnetic field measurement
General
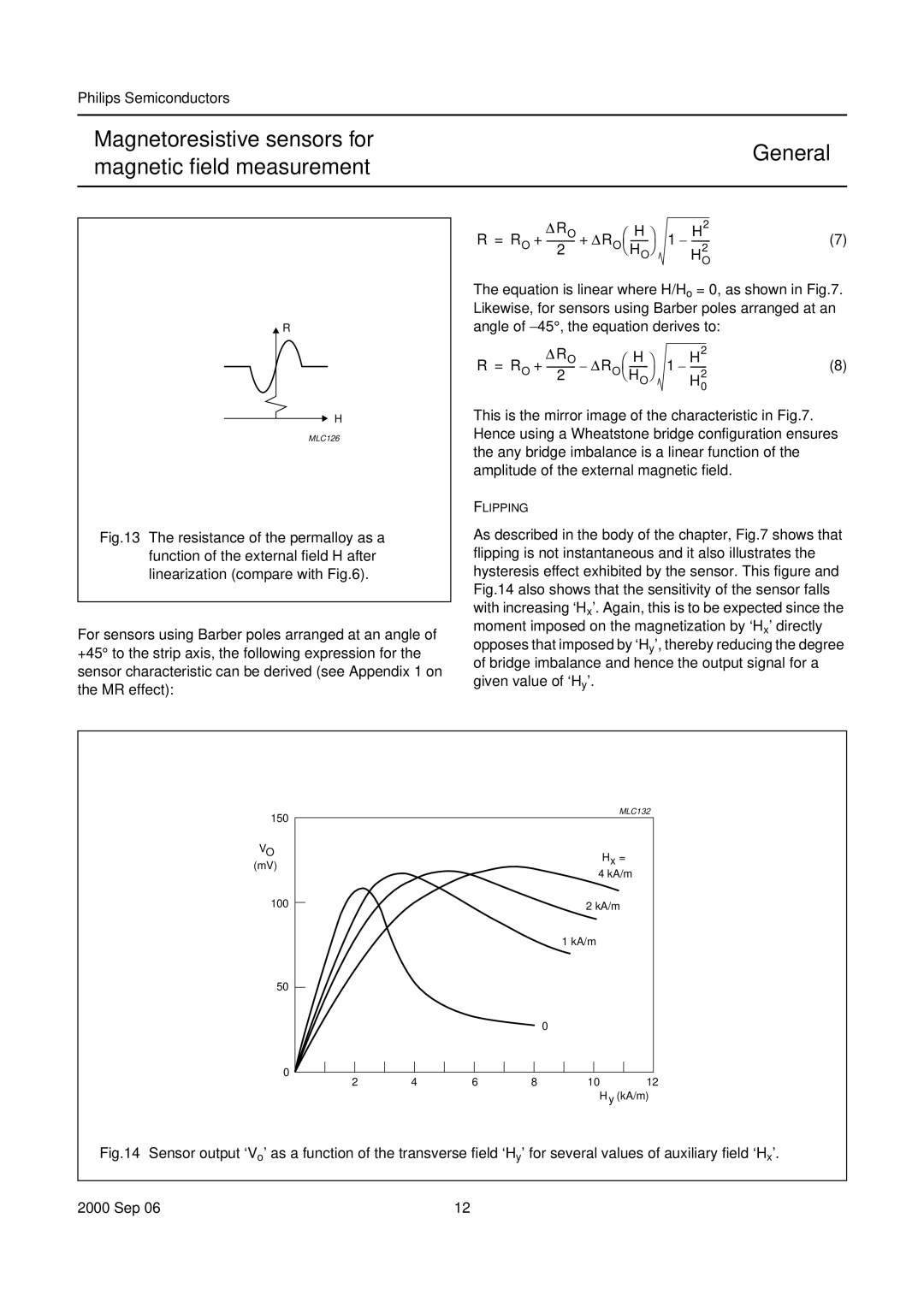
handbook, halfpage | R |
|
H
MLC126
Fig.13 The resistance of the permalloy as a function of the external field H after linearization (compare with Fig.6).
For sensors using Barber poles arranged at an angle of +45° to the strip axis, the following expression for the sensor characteristic can be derived (see Appendix 1 on the MR effect):
R = R |
| ΔRO | + ΔR | ⎛ H | ⎞ | 1 | H2 | (7) |
O | + | ⎠ | ||||||
| 2 |
| O ⎝ H |
| 2 |
| ||
|
|
|
| O |
|
| HO |
|
The equation is linear where H/Ho = 0, as shown in Fig.7. Likewise, for sensors using Barber poles arranged at an angle of −45°, the equation derives to:
R = R |
| ΔRO | ⎛ H | ⎞ | 1 | H2 | (8) | |
O | + | ⎠ | ||||||
| 2 |
| O ⎝ H |
| 2 |
| ||
|
|
|
| O |
|
| H0 |
|
This is the mirror image of the characteristic in Fig.7. Hence using a Wheatstone bridge configuration ensures the any bridge imbalance is a linear function of the amplitude of the external magnetic field.
FLIPPING
As described in the body of the chapter, Fig.7 shows that flipping is not instantaneous and it also illustrates the hysteresis effect exhibited by the sensor. This figure and Fig.14 also shows that the sensitivity of the sensor falls with increasing ‘Hx’. Again, this is to be expected since the moment imposed on the magnetization by ‘Hx’ directly opposes that imposed by ‘Hy’, thereby reducing the degree of bridge imbalance and hence the output signal for a given value of ‘Hy’.
150
VO (mV)
100
50
0
MLC132
Hx = 4 kA/m
2 kA/m
1 kA/m
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 | 4 | 6 | 8 | 10 | 12 | ||||||||
|
|
|
|
|
|
|
|
|
|
| H y (kA/m) | ||
Fig.14 Sensor output ‘Vo’ as a function of the transverse field ‘Hy’ for several values of auxiliary field ‘Hx’.
2000 Sep 06 | 12 |