HP Part Number NW239-90001 Edition 1, May
HP 10bII+ Financial Calculator User’s Guide
Legal Notice
HP 10bII+ Financial Calculator
Number
Keyboard Map Legend
Table of Contents
Page
Page
III
JGD
At a Glance
Basics of Key Functions
Boxed Key Functions
Shift Keys
JV§4
Jj7V1
Percentages
Add 15% to
GG¼
JVÀ
DDÃ
Memory Keys
GG4
GV4
J7GV
DSÙ
JG\Í
JYÏ
Time Value of Money TVM
D7VÒ
JyÌ
TVM What if
How much can you borrow at a 9.5% interest rate?
Jæjg
Amortization
Amortize the 1 st through 24 th loan payments
Depreciation
Interest Rate Conversion
Cash Flows, IRR/YR, NPV, and NFV
\½\«
Yj¤
Yy¤
JÆG¤
GD¤
G7GgGJ
VG4
Date and Calendar
Bonds
S7jVÎ
Y7jVÔ
For more information on bond calculations, refer to , Bonds
Break-even
\T \«
\k \«
\h \«
\e \«
YÆd¡
GÆV¡
SÆJS¡
\T\«
7VF
\5V
17GV4
Probability
7SG
Trigonometric Functions
Find Sin θ =.62 in degrees. If RAD is displayed, press
\aJg
Convert the results to radians using Pi
At a Glance
Getting Started
Power On and Off
Manual Conventions and Examples
Displayed text
Item before the / is the alternate
Shift Keys
JdPJG7Sg4
GY7jJ1SG7Yj4
Simple Arithmetic Calculations
Operating Modes
1JJV7V4
Calculations in Chain Mode
S7dPV7DVa
7dJ4
Using Parentheses in Calculations
Calculations in Algebraic Mode
Da\qgVA
JG\n
AD4
JVy
Understanding the Display and Keyboard Cursor
Clearing the Calculator
Annunciators
Clear All
Clearing Messages
INV
Swap Key
Input Key
Statistics Keys
Same as pressing
D7Vj1G7DS\b
Gd7GV\B
Math Functions
One-Number Functions
Getting Started
JVc
\5Y
J1SC
7DVoR
\5G
A7SGoR
YP\
PY7V\2
17VdrC
J7GVrc
Two-Number Functions
In-line Functions
JjÆ
Jj\¨
Gd\¨
Gd1DD
-23below lists the two-number functions of the calculator
Arithmetic with One-and Two-number Functions
JGV\QD4
G7V\K
\Qv4
VAJ7GV4
GG1JY\¨
Last Answer
YV7SP
\5D
7JGVS4
Specifying Displayed Decimal Places
Jaj4
\54
\zyJG
Messages
D7gjSVYD
Business Percentages
GV§
Business Percentage Keys
Percent key
GdJ7j\¨
JGV1j§
DJS7g4
Jgpvæ
JdÀ
Gvvà
Margin and Markup Calculations
Margin Calculations
Using Margin and Markup Together
D7SÀ
JVÃ
Using Constants
Using Stored Numbers in Calculations
V1Gª
Number Storage and Storage Register Arithmetic
\QDª
J1J§ª
Example Calculate 10 + 10%, 11 + 10%, and 25 + 10%
Example Calculate 23
Using the M Register
VV\¨DGª
YV4
Jjs
Using Numbered Registers
JY7GVm
JS7dVm
\w7Y ADd7JV \wG
YjV7S
VS7J1
V7Y
YV7j \wD
G7V
\wPD
How to approach a Financial Problem
Picturing Financial Problems
Periods and Cash Flows
Signs of Cash Flows
Simple and Compound Interest
Simple Interest
Compound Interest
Interest Rates
Recognizing a TVM Problem
Two Types of Financial Problems
Cash flow diagram Borrower’s perspective
Recognizing a Cash Flow Problem
Cash flow diagram Investment in a mutual fund
Using the TVM Application
Time Value of Money Calculations
TVM Keys
Loan Calculations
Begin and End Modes
J7VÒ
Dpjgù
Jyva
JVÏ
1VÌ
DjVyÌ
1JV4
J7VÒ
DDyÌ
1JG4
GV\Ú
JjGVÏ
G7gÒ
YgÙ
1vÌ4
Savings Calculations
J7GÒ
GyÏ
GyÌ
GY\Í
S7DÒ
JV\Ú
YyÏ
Lease Calculations
Cash flow diagram Calculate the monthly lease payment
JVÉ
Cash flow diagram Calculate PV of the lease
GYyÌ
YjÙ
1vÌy4
Step Find the present value of the buy option
JVyÉ
1p4
Step Add the results of ’ ’ and ’ ’
Amort key on the HP 10bII+ allows you to calculate
To Amortize
J7jVÒ
Jdægy
JJ7VÒ
Jygvï
GVÆ
VYÆ
Amortize the 1st, 25th, and 54th payments
Interest Rate Conversions
S7j\Ó
Investments With Different Compounding Periods
First Bank
S7SD\Ó
S7SV\Ó
DS\Í
Compounding and Payment Periods Differ
GVyÌ
DSV\Í
Resetting the TVM Keys
Depreciation Keys
Depreciation
Item in the selected format
Inputs 5 for the expected useful life
Depreciation example using Declining Balance Keys
Cash Flow Calculations
How to Use the Cash Flow Application
Number1 ¤
Clearing the Cash Flow Memory
Cash Flow Calculations
Vy¤
Gy¤
Calculating Internal Rate of Return
AJG
JJjSV7Gd¤
NPV and IRR/YR Discounting Cash Flows
Organizing Cash Flows
Initial cash flow and cash flow groups
JJy¤
Viewing and Editing Cash Flows
11GÆ
JVÆ1GÆ
1JGyÆ1G
Calculating Net Present Value and Net Future Value
ÆY¤
VÆJ¤
VÆG¤
Æd¤
JVÆJ¤
JÆJ¤
JVÒ
Automatic Storage of IRR/YR and NPV
Cash flow diagram Calculates NPV
Calendar Formats and Date Calculations
Calendar Format
Date Format
Using the Input key
Date Calculation
Date Calculations and Number of Days
JG7JgGJJ
To enter the data for this example using the Ækey
\ÇJ4
ÆJ\Ç
Y7SGJ\Ä
\5S
DJ7JGJ4
J7JjGJG
Using the Ækey
J7JjGJGÆ
S7YGJV\Ä
Bond Keys
Bonds
Y7GgGJ
V7VÎ
S7YGG
JYË
JJÑ
Resetting the bond keys
J7JVGG
Y7JVGJG
Break-even Keys
Break-even
Break-even example
Calculating the projected maximum fixed cost
Resetting the Break-even keys
\h\«
\k\«
\e\«
\Z\«
Entering Statistical Data
Clearing Statistical Data
One-Variable Statistics
Two-Variable Statistics and Weighted Mean
Viewing and Editing Statistical Data
DGÆYJV¡
DVÆVJV¡
YD\W\5G
YDÆJGD¡
DjÆSgV¡
YV\W
Summary of Statistical Calculations
D7GV¡
Y7V¡
D7V¡
D7jV¡
JgGÆgJ¡
JdDÆd¡
JjjÆgD¡
JgVÆjj¡
400
JÆdG¡
GÆJY¡
DÆJJ¡ VÆGGSV¡
VÆGgd¡
Weighted Mean
VVÆDG¡
VÆVY¡
VJÆgg¡
VJSÆdG¡
Probability Calculations
Factorial
Permutations
VÆD
VD4
V9D4
VÆD9
Advanced Probability Distributions
YG\w6
Normal Lower Tail Probability
J7jyF
Inverse of Normal Lower Tail Probability
7GVoF
GIJ7gSy4
GÆJ7gSyI
Students T Probability Lower Tail
GSoI7V4
GSÆ7VoI
Inverse of Student’s t Probability Lower Tail
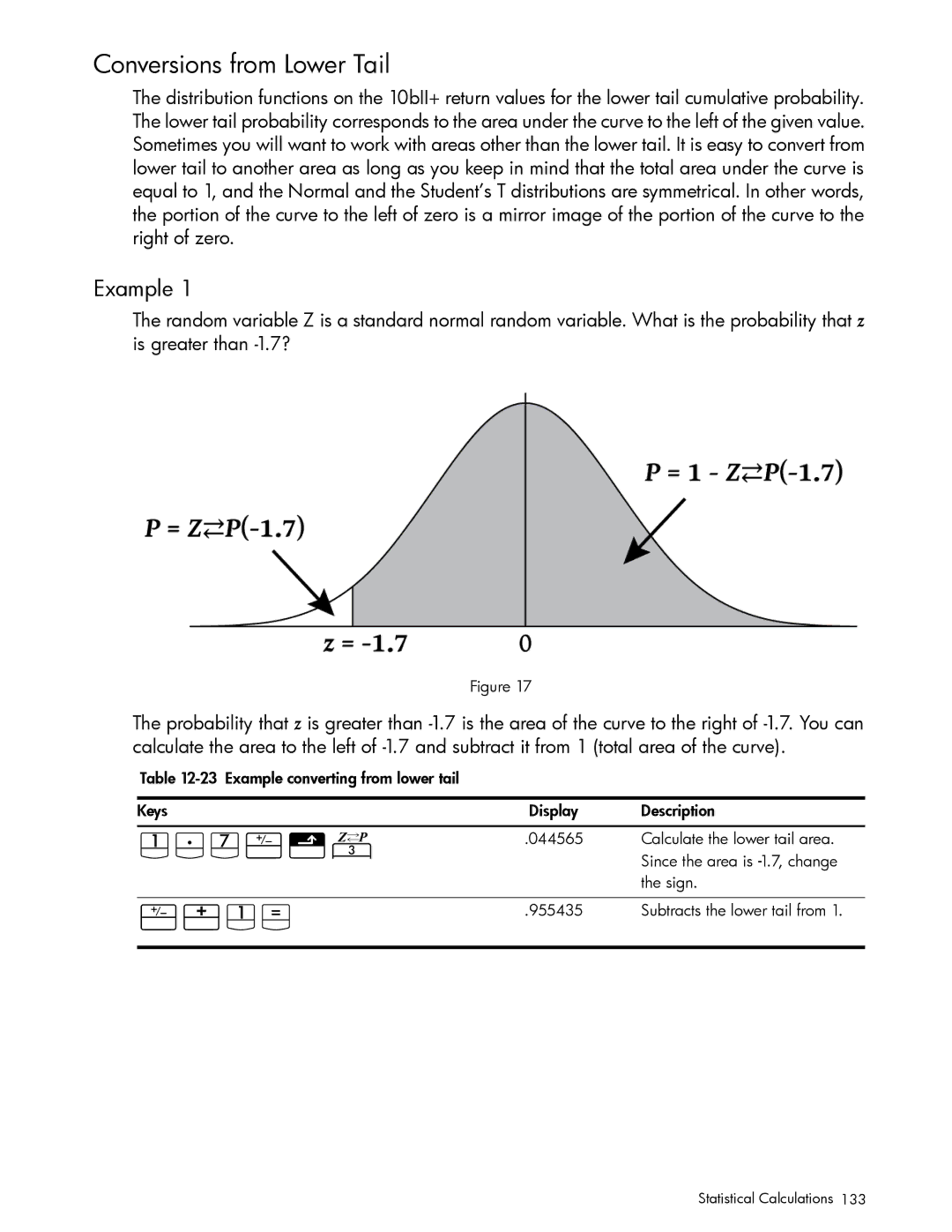
Conversions from Lower Tail
Y1J4
PG4
J7GyF
Returns desired value of z
Statistical Calculations
\qJ1\q GaJ4
Setting a Sales Price
Additional Examples
Business Applications
GÆJJGJ¡
JÆJ¡
DÆJDS¡
YÆJSjV¡ VÆGVd¡
\q\qJ AG\n
Gpdspj
\qDA
YVsPJ§
Jg§
AJPJ4
YVjG7gy
Yield of a Discounted or Premium Mortgage
JdyÏ
VÙAYGÙ
G7VÒ
Annual Percentage Rate for a Loan With Fees
AG§Ï
JSÏ
JGÒ
AD§Ï
JSaDP
AJGP
YV\Ǥ4
1YVÏ
D7VÒ
Jgvï
PvÙ4
Jjvï
JDÏ
JG\Ó
ÉD\Ú
Canadian Mortgages
JJ7GÒ
DVVVyÌ
What if … TVM Calculations
PvÙ1
GS\Í
VÏ4
Savings
Stores effective rate as annual
Gains That Go Untaxed Until Withdrawal
Jyyù
DVÙ
PJV§4
Yòìï
DyÌ
G7JjVAGg
Cash Flow Examples
Wrap-Around Mortgages
GGVJ7GG
Cash flow diagram Wrap-around mortgage
VÌyAjVY
DVy¤
GG\¥
VÌy¤
Low Power Annunciator
Power and Batteries
Installing Batteries
Appendix a Batteries and Answers to Common Questions
Resetting the calculator
Determining if the Calculator Requires Service
Calculator won’t turn on
Erasing the calculator’s memory
Answers to Common Questions
See Determining If the Calculator Requires Service
Environmental Limits
Appendix B More About Calculations
IRR/YR Calculations
Equations
Time Value of Money TVM
Payment Mode Factor S = 0 for End mode 1 for Begin mode
Amortization
Interest Rate Conversions
Cash-Flow Calculations
For more than one coupon period to redemption
Bonds
Statistics
Depreciation
Forecasting
Memory has been erased Ch
Appendix C Messages
Cashflow memory was cleared
Tvm registers were cleared
Statistical memory and registers were cleared
Bond registers were cleared
HP Limited Hardware Warranty and Customer Care
Warranty, Regulatory, and Contact Information
Limited Hardware Warranty Period
Replacing the Batteries
Exclusions
General Terms
Modifications
Canadian Notice
Avis Canadien
European Union Regulatory Notice
Germany
Customer Care Contact Information
Perchlorate Material special handling may apply
香港特別行
Tobago Tunisia Turkey Türkiye Turks 01-800-711-2884
ไทย
Warranty, Regulatory, and Contact Information
Warranty, Regulatory, and Contact Information
Battery
Advance payments Algebraic mode
Chain mode
Error messages Factorial
Interest rate conversions Investments
In-line functions Interest
Keyboard
Keys
Warranty
Trigonometric functions Troubleshooting
Modes
Operating modes Parentheses