User Guide
HP Prime Graphing Calculator
Product Regulatory & Environment Information
Edition1 Part Number NW280-2001 Legal Notices
Edition
Printing History
July
Page
Contents
Plot view
Application Library App views Symbolic view
Common operations in Plot view Zoom Trace
Function app
Computed statistics
233
Getting started with the Polar app 277
Getting started with the Parametric app 271
Variables
Lists
Status messages
Basic integer arithmetic
Manual conventions
Preface
Function, Polar, Parametric, Ans, etc
Before starting
Getting started
On/off, cancel operations
Display
Sections of the display
Uppercase when a key is pressed
Be entered in uppercase when a
Lowercase when a key is pressed
You are working in CAS view, not
Navigation
Touch gestures
Keyboard
Context-sensitive menu
Primary entry and edit keys are
Entry and edit keys
Comparison operators and Bool
Minute, or second symbol accord
Ean operators
Characters
Shift keys
Adding text
Math template
Math keys
Math shortcuts
236…. Press conce to see 219602 and again to see
Fractions Hexagesimal numbers
Pressing ca third time will cycle back to
Original decimal representation
Return home H Enter 4BQ13 s6B23n 3BQ5
EEX key powers
To select from a menu
Menus
Toolbox menus
Input forms
Alternatively, select the field and tap
Home settings
System-wide settings
Fixed 2 format
Becomes 123.46
23E2 in Scientific
Becomes 1.23E9 in Engineer
Or a+b*i
Shorthand. The default is to provide
Commands on the Math and CAS
Menus are presented descriptively
Or in common mathematical
MM/DD/YYYY
YYYY/MM/DD, DD/MM/YYYY, or
Press SH Settings to open
Specifying a Home setting
Always one-dimensional
Where to start
Mathematical calculations
Choosing an entry type
Entering expressions
Examples that follow assume that the entry mode is
RPN Reverse Polish Notation. Not available in CAS view
Textbook
R23jw14S j8nQ3 h45E
Example Parentheses
Algebraic precedence
Negative numbers
E45+Sz
Sj85s9
Explicit and implied multiplication Large results
Reusing previous expressions and results
To reuse the last
Using the clipboard
Result
Sj2E
Storing a value in a variable
SjS+E
Szj AQAcE
Szj AaE
Example To assign π2 to to the variable a
Sharing data
Complex numbers
R2o3 Ay6E
HP Prime to another
When is tapped
Online Help
RPN Reverse Polish Notation
Reverse Polish Notation RPN
RPN is available in Home view, but not in CAS view
History in RPN mode
Sample calculations
Re-using
Results
SzX3
Reverse Polish Notation RPN
Swap
Manipulating the stack
Stack
Show an item Delete an item Delete all items
CAS view
Computer algebra system CAS
Menu buttons in CAS view are Assigns an object to a variable
CAS calculations
2Asj+3
Settings
Asw2
5Asjw6
Standard or Scientific or Engineering
Ments Radians or Degrees
Recursive Replacement
Tion above
See also Recursive Evalua
Computer algebra system CAS
Computer algebra system CAS
Exam Mode
Press SH. The Home Settings screen appears Tap
Modifying the default configuration
Don’t want disabled are not selected
Press O+ A+ c
Before, the only base configuration will be Default Exam
Creating a new configuration
Activating Exam Mode
Tap If a configuration other than Default
To activate exam mode
Cancelling exam mode
Modifying configurations
To change a configuration
Deleting configurations
To return to the default configuration
Tap Exam Mode screen appears
Exam Mode
An introduction to HP apps
Equations
Linear Solver
Solve Explore equations in one or more real
Application Library
To delete an app Other options
App views
Symbolic view
Confidence level, and select a type
Test
Symbolic Setup view
Plot view
Symbolic view
Solve
Plot Setup view
Numeric view
Test selected in Symbolic view
Advanced View a table of numbers generated by Graphing
Symbolic view, and set the zoom factor
Numeric Setup view
Advanced Specify the numbers to be calculated Graphing
Open the app
Quick example
4Szf n2f jE
N2f
Press SP Set the second θRNG field to 4π by entering
Press P
Press Pto return to Plot view and see the complete plot
Θ column to be 1. You set this up in the Numeric Setup view
Common operations in Symbolic view
Numeric View
Modify a definition
Add a definition
Definitional building blocks
From Home variables
Select or deselect a definition to explore
Evaluate a dependent definition
F9X=X2+Statistics2Var.PredY6
X2+X+ 2 *X2
Delete a definition
Choose a color for plots
Symbolic view Summary of menu buttons
Override system-wide settings
Common operations in Symbolic Setup view
Restore default settings
Press SYto open Symbolic Setup view
Zoom
Common operations in Plot view
Zoom factors Zoom options
Zoom setting
By the X Zoom and Y Zoom settings
Center on
Shortcut press w
Graph with the original plot settings
Given the supplied x axis settings. For
Shows a representative piece of the plot
Apps, autoscaling rescales both axes
Zoom with
Testing a
Split-screen
Viewing
Out
Shown, tap
Autoscale
Square
Decimal
Integer
Trig
Trace
To evaluate a definition To turn tracing on or off
Configure Plot view
Common operations in Plot Setup view
Plot view Summary of menu buttons
Polar only
Parametric Only
Sequence Only
Stats 1 Var only
That here are two fields one for
Sets the initial range of the x-axis. Note
Panning and zooming
Sets the initial range of the y-axis. Note
Graphing methods
Common operations in Numeric view
Restore default settings
Zoom options Zoom keys Zoom menu
Evaluating
Deleting data
Custom tables
Start typing a new value Only visible if Numtype is set to
Numeric view Summary of menu buttons
Select Ascending or Descending ,
Modifying Numeric Setup
Common operations in Numeric Setup view
Adding a note to an app
Combining Plot and Numeric Views
Creating an app
Fibonacci in this example
Asjw5
App functions and variables
Select Statistics 1Var results MeanX
Tap This opens a menu of app variables
Getting started with the Function app
Function app
Rdw1 jw3E
Open the Function app Define the expressions
Open the Function app ISelect
Function
Set up the plot Plot the functions
Trace a graph Change the scale
Display the Numeric Setup view SMSetup
Display Numeric view Set up Numeric view
Explore Numeric view
Press SJClear to reset all the settings to their defaults
To navigate around a table
Substituted the values in the X column for x
To go directly to a value
To access the zoom
Options
Display the Plot view menu
Analyzing functions
To find a root of the quadratic function
=or\
Intersection of two
To find an
Functions
Intersection
To find the slope of the quadratic function
To find the signed area between the two functions
To find
Function Variables
Extremum
Quadratic
Function Select Results and then the variable of interest
Tap and select
Named Extremum
Summary of FCN operations
Slope
Advanced Graphing app
Getting started with the Advanced Graphing app
Jn2
Open the app Define the open sentence
+ n5
ISelect Advanced Graphing
128 Advanced Graphing app
Advanced Graphing app 129
Region. Use this option for
You can move in any direction within
Inequalities, for example
Edge
Numeric view Display the Numeric view Explore Numeric view
Trace in Numeric view
Numeric Setup
Sj3n2
Trace Edge
Trace PoI
Exploring a plot from the Plot Gallery
Plot Gallery
Getting started with the Geometry app
Geometry
Plot Function
3seASsE
With plotfunc on the entry line, enter 3*sinx
More Tangent
Derivative point
Create a
AbscissaGB,slopeGC
Add some calculations
140
Derivative
Plot view in detail
Point D is the point whose ordinate value matches
Derivative changes by looking at a plot of it rather than
142
Object
Selecting an
Hiding names
Moving objects
Filling objects
Coloring objects
Removing fill
Undoing
Clearing all
Clearing an
Objects
Moving about
Plot view buttons and keys
Key Result in Plot view
Symbolic view in detail
Entries
Re-ordering
Hiding an object
Tap either To move it down the list or Move it up
Numeric view in detail
Can delete an object in Symbolic view
Deleting an
Tap Or press C To delete all objects, press SJ
Enter radiusGC
Listing all
152
Points
Geometric objects
More
Element 0 . . Notice
Line
Ngon
Polygon
Special
Curve
That passes through each
Circumcircle is the circle
Triangle’s three vertices
Thus enclosing the triangle
Special Locus places
Geometric transformations
Axis and press E. The object is reflected across
Tap Select Reflection
Symmetry axis defined in step
Given scale factor around a given point as center
GK,angleGK,GL,GM
Select Transform Rotation
164
Symbolic view Cmds menu
Geometry functions and commands
Point
Barycenter
Divisionpoint
Center
Element
Inter
Midpoint
Isobarycenter
Orthocenter
Point
Stop trace
Point2d
Erase trace
DrawSlp
Exbisector
Bisector
Halfline
Line
Parallel
Medianline
Perpenbisector
Medianlinepoint1, point2, point3
Segment
Perpendicular
Tangent
Draws a segment defined by its endpoints
Hexagon
Equilateraltriangle
Equilateral triangle0,6 draws an equilateral
Equilateral triangle0,6, v draws an equilateral
Isopolygon
Isoscelestriangle
Parallelogram
IsoscelestriangleGA, GB, angleGC, GA, GB
Quadrilateral
Polygon
Rectangle
Rhombus
Square
Righttriangle
Triangle
Circumcircle
Circle
Conic
CircumcircleGA, GB, GC draws the circle
Excircle
Ellipse
Hyperbola
Excirclepoint1, point2, point3
Incircle
Transform
Locus
Parabola
Projection
Inversion
Reflection
Draws the orthogonal projection of a point onto a curve
Similarity
Rotation
Translation
RotateGA, angleGB, GC, GD,GK rotates
Measure Plot
Measure
Numeric view Cmds menu
Angle
Affix
ArcLen
Area
Distance
Coordinates
Distance2
Area4-x2/4, x=-4..4 returns 14.666…
Extractmeasure
Equation
Ordinate
Parameq
Radius
Test
Iscollinear
Isconcyclic
Isequilateral
Iselement
Isisoceles
Isorthogonal
Isparallelogram
Isparallel
Isperpendicular
Isrectangle
Issquare
Other Geometry functions
Convexhull
Harmonicconjugate
Isharmoniccirclebundle
Isharmonic
Isharmoniclinebundle
Isrhombus
LineVert
LineHorz
Openpolygon
Polar
Pole
Powerpc
Radicalaxis
Reciprocation
Vector
Singleinter
Vertices
Verticesabca
194
Getting started with the Spreadsheet app
Spreadsheet
To open the Spreadsheet app, press Iand select Spreadsheet
196
Select cell C3 Enter a label for your total commission
Select cell D1 Enter a formula to add up your takings
Select the heading cell for column C, tap and select
Select cell C5
Enter a label for your fixed costs
Ancostse
Navigation, selection and gestures
Basic operations
Cell naming
Cell references
Method
Enter Cost and tap
Entering content
COST*0.33 and tap
Enter Statistics1Var.D1
Select Polynomial Find Roots
External functions
Copy and paste
External references
To copy one or more cells, select them and press SVCopy
Format, both value and format, or both formula and format
Referencing variables
= Row2-√Row-1. The only
Using the CAS in spreadsheet calculations
Handled by the CAS, but only Evaluates it
Buttons and keys
Line is active
Changes to
Formatting options appear
Formatting options
Font Size Auto or from 10 to 22 point
Format Parameters
Spreadsheet functions
Getting started with the Statistics 1Var app
Statistics 1Var app
Statistics 1Var
Sample data in D1
Menu items you can tap on in Symbolic view are
Symbolic view menu items
Editing. Tap when done
Enters D directly to save you having to press two keys
214
Entering and editing statistical data
Configure a histogram plot for the data Setup
1Var app open, return to Home view and enter
Edit a data set
Spreadsheet.A1A10 D7 E
Menu items you can tap on in Numeric view are
Delete data Insert data Generating data Sort data values
Computed statistics
Plot types
Plotting
To plot statistical data
Histogram
Normal probability
Box-and-Whisker
Line plot
Bar graph
Pareto chart
Setting up the plot Plot Setup view
Exploring the graph
Data in descending
Menu items you can tap on in Plot view are
Plot view menu items
Getting started with the Statistics 2Var app
Statistics 2Var app
Advertising minutes Resulting sales $
Dependent, y
Enter the advertising minutes data in column C1 2E1E3E5E5E4
Statistics 2Var
Statistics 2Var app 225
Setup plot Plot the graph
Display the equation Predict values
Spreadsheet.A1A10 C7 E
Buttons you can tap on in Numeric view are
Numeric view menu items
Tap , make your change, and tap
Descending
Delete data Insert data Sort data values
Fit types
Defining a regression model
Fits the data to a logistic curve
Where L is the saturation value
For growth. You can store a
Positive real value in L, or-if
COV
SCOV
ΣXY
SerrY
Plotting statistical data
Tracing a curve
Tracing a scatter
Tracing order
Plot view menu items
Plot setup
Plotting mark
Connect
Home view
Predicting values
Troubleshooting a plot
Getting started with the Inference app
Inference app
Open
Inference
Test μ1 μ2, the T-Test on
Symbolic view options
Test 1 μ from the Type menu
Select the inference method Enter data
Sample mean Sample size
Population standard deviation Alpha level for the test
Display the test results Plot the test results
Open the Statistics 1Var app Clear unwanted data Enter data
Importing statistics
82.5 E 83.1 E 82.6 E 83.7 E 82.4 E 83 E
Select inference method and type Import the data
Calculate statistics Open the Inference app
Tap on the Method field and select
Confidence Interval
Display
Hypothesis tests
Results
Numerically
Menu name
One-Sample Z-Test
Inputs
Two-Sample Z-Test
One-Proportion Z-Test
Two-Proportion Z-Test
Test Z Test statistic Test Δ pˆ Difference between
One-Sample T-Test
With the test Z-value
This test measures the strength of the evidence for a
Test μ1 μ2
Two-Sample T-Test
Each sample from a different population, this test
Sample 2 standard deviation
Sample 1 standard deviation
Α level that you supplied
One-Sample Z-Interval
Confidence intervals
Two-Sample Z-Interval
Int 1π
One-Proportion Z-Interval
Number of successes
Sample success count Sample size Confidence level
Menu name Int π1 π2
Two-Proportion Z-Interval
Confidence interval for the difference between
Proportions of successes in two populations
Two-Sample T-Interval
One-Sample T-Interval
Result Definition
258
Getting started with the Solve app
Solve app
Open the Solve app
One equation
Clear the app and define the equation
AVjS.AU j+2AAAD
Solve the unknown variable
Enter known variables
Kph over a distance Is approximately 2.4692 m/s2
Plot the equation
Where n is the number of the selected equation
Select Auto Scale Select Both sides of En
Matches the value of a you calculated above
Open the Solve app Define the equations Enter a seed value
Several equations
AXj+AYj S.16E AXwAYS. Q1E
Solve the unknown variables
Limitations
Zero
Solution information
Sign
Reversal
No values satisfy the selected equation or expression
Bad Guesses Constant?
Value of the equation is the same at every point sampled
Getting started with the Linear Solver app
Linear Solver app
Open the Linear Solver app. ISelect
Linear Solver
Coefficients and constants had been entered
Define and solve the equations
Solve a two-by- two system
Menu items
270
Getting started with the Parametric app
Parametric app
Open the Parametric app
Parametric
8ed? 8fd?
Define the functions
Degrees
Set the angle measure Set up the plot Plot the functions
274
Tap .The table scrolls to the value you entered
276
Polar app
Open the Polar app ISelect Polar App opens in Symbolic view
Getting started with the Polar app
Open the Polar app
5Szf dn2 fdj
Set angle measure Set up the plot
Define the expression 5πcosθ/2cosθ2
Plot the expression Explore the graph
280 Polar app
Getting started with the Sequence app
Sequence app
+ E
App opens in Symbolic view Define the Fibonacci sequence
Open the Sequence app ISelect
Sequence
Select Stairstep from the Seq Plot menu
Plot the sequence
Display Numeric view Explore the table of values
Define the expression Setup the plot
Set up the table of values
Another example Explicitly-defined sequences
RQFand
Plot the sequence Explore the table of sequence values
Getting Started with the Finance app
Finance app
288
Cash flow diagrams
Time value of money TVM
PMT
TVM calculations Another example
292
To calculate amortizations
Calculating amortizations
Amortization graph
Finance app 295
Getting started with the Triangle Solver app
Triangle Solver app
Tapping
Open the Triangle Solver app ISelect
Specify the known values
Solve for the unknown values
Choosing triangle types
Special cases
Triangle Solver app 299
Linear Explorer app
Explorer apps
Between them by tapping or
Graph mode
Test mode
Equation mode Tap to enter
Open the app
Quadratic Explorer app
Quadratic
Explorer
Its value. When you are ready, tap To see if you
Equation mode
Tap To see the correct answer and tap Exit Test mode
Graphs that are harder match by tapping Respectively
Trig Explorer
Trig Explorer app
Graph by pressing
Tap To switch to
Cursor keys. All four keys
Are available.
Now press the cursor keys to select each parameter
Tap to see the correct answer and tap to exit Test mode
All the functions and commands
Functions and commands
308
Abbreviations used in this chapter
Keyboard functions
NORMALICDFμ,σ,p
Shex
+,w,s, n
E5 returns
ALOG3 returns
Efg
+2*i returns -1-2*i
1returns
2returns
Numbers
Math menu
Example XPON123456 returns 5 since 105.0915... equals
Arithmetic
Maximum Maximum. The greater of two values
Modulus Modulo. The remainder of value1/value2
Example ARG3+3*i returns 45 degrees mode
Percentage x percent of y that is, x/100*y Example
Trigonometry
Probability
Hyperbolic
Normal Random real number with normal distribution Nμ,σ
PERM5,2returns
NORMALDμ,σ,x
RANDSEEDvalue
NORMALD0.5 and NORMALD0,1,0.5 both return
STUDENTn,x
Is a real number
CHISQUARECDF2,6.1 returns
CHISQUARECDFn,k
FISHERCDFn,d,x
FISHERCDF5,5,2 returns
List
Special
Matrix
Algebra
CAS menu
PartfracRatFrac or Opt
Syntax substExpr,Var=value
Numera,b
Denoma/b
DiffExpr,var DiffExpr,var1$k1,var2$k2
Calculus
LimitExpr,Var,Val,Dir1, 0
SumExpr,Var,Real1, Real2,Step
SeriesExpr,Equalvar=limitpoint,Orde r,Dir1,0,-1
CurlExpr1, Expr2, …, ExprN, Var1, Var2, …, VarN
DivergenceExpr1, Expr2, …, ExprN, Var1, Var2, …, VarN
Hessian Returns the Hessian matrix of an expression
GradExpr,LstVar
HessianExpr,LstVar
IbpufVar, uVar, Var, Real1, Real2
SumriemannExprXpr,Lstvar1,var2
PrevalExprFvar,Reala,Realb,Var
TaylorExpr,Var=Value,Order
DivpcPoly1,Poly2,Integer
Solve
Zerosx2-4 returns -2
ZerosExpr,Var or zerosExpr1, Expr2,…,Var1, Var2,…
CsolveEq,Var CsolveEq1, Eq2,…, Var
CZerosExpr,Var CZerosExpr1, Expr2,…,Var1, Var2,…
Rewrite
Exp2powExpr
TexpandExpr
Pow2expExpr
Exp2trigExpr
Sin2costanExpr
Asin2atanExpr
Acos2asinExpr
Acos2atanExpr
Atan2asinatan2*x returns
Atan2asinExpr
Atan2acosExpr
Tan2sincosExpr
TrigtanExpr
TrigcosExpr
Atrig2lnExpr
TlinExprTrig
Integer
IsPrimeInteger
GcdIntgr1, Intgr2,…
NextprimeInteger
PrevprimeInteger
IquoIntgr1, Intgr2
Polynomial
IremIntgr1, Intgr2
Powmoda, n, p,Expr,Var
DivisPoly or divisPoly1, Poly2,…
CoeffPoly, Var, Integer
FactorsPoly or factorsPoly1, Poly2,…
GcdPoly1,Poly2
Poly2symbVector, Var
Symb2polyExpr,Var Symb2polyExpr, Var1, Var2,…
PcoefVect
QuoList1, List2, Var QuoPoly1, Poly2, Var
PminMtrx,Var
RemList1, List2, Var RemPoly1, Poly2, Var
DegreePoly
ContentPoly,Var
FactorxnPoly
SturmabPoly,Var,a,b
GbasisPoly1 Poly2…, Var1 Var2…
CyclotomicInteger
GreducePoly1, Poly2 Poly3 …, Var1 Var2…
HermiteInteger
LaguerreInteger
LagrangeX1 X2…, Y1 Y2…
Tchebyshev1Integer
Tchebyshev2Integer
Plot
PlotodeExpr, Var1, Var2, X0, Y0
App menu
PlotlistX1, Y1, X2, Y2, …
Function app functions
Spreadsheet app functions
Solve app functions
SOLVEEn,var,guess
SOLVEX2-X-2,X,3returns2
=STAT1A25A37
FunctionNameinput,optional Parameters
=STAT1A25A37,h n
As in SUMB7C23
For example, AVERAGEB7B23 returns the arithmetic
Calculates the arithmetic mean of a range of numbers
Specify a block of cells, as in AVERAGB7C23
Finance app
Columns are multiplied to generate a data point
Second column is treated as the weight of the first
Set to
Place column headers Place row headers Serr
STAT1A25A37
REGRSInput range,model, configuration
STAT1A25A37,h n x σ
Example REGRSA25B37,2
PredX
PredY
PredYmode, x, parameters
PredXmode, y, parameters
HypZ1mean The one-sample Z-test for a mean
HypZ1mean x, n,μ0,σ,α,mode, configuration
HypZ1mean0.461368, 50, 0.5, 0.2887, 0.05
HypZ2mean0.461368, 0.522851, 50, 50, 0.2887, 0.2887, 0.05
HypZ1prop
HypZ1propx,n,π0,α,mode
HypZ1prop21, 50, 0.5, 0.05,1
HypZ2prop
HypT1mean x ,s,n,μ0, α,mode,configuration
Mode Specifies which alternative hypothesis to use ≠ μ0
HypT1mean The one-sample t-test for a mean
HypZ2prop21, 26, 50, 50, 0.05
ConfZ1mean x ,n,s, C,configuration
HypT2meanx1,x2,s1,s2, n1,n2, α,pooled,mode, configuration
ConfZ1propx,n,C,configuration
ConfZ2mean x1, x2, n1, n2,s1,s2,C, configuration
ConfZ1mean0.461368, 50, 0.2887
ConfZ2mean0.461368, 0.522851, 50, 50, 0.2887, 0.2887
ConfT1mean
ConfZ2prop
ConfZ1prop21, 50
Statistics 1Var app functions
ConfT2mean x1, x2, s1,s2,n1, n2,C,pooled, configuration
ConfT1mean0.461368, 0.2776, 50
ConfT2mean0.461368, 0.522851, 0.2776, 0.2943, 50, 50, 0
SetFreq
Do1VStats
SetSample
Resid
Statistics 2Var app functions
Do2VStats
SetDepend
SetIndep
Inference app functions
DoInference
HypZ1mean
Critical value of π associated with the critical Z-value
Test π value
HypZ2mean x1, x2, n1, n2,σ1,σ2,α,mode
Order
HypT1mean
Test Δπ value
Critical value of the statistic associated with
HypT2meanx1,x2,s1,s2, n1,n2, α,pooled,mode
ConfZ2mean
ConfZ1mean
ConfZ1prop
Two proportions. Returns a list containing in order
CalcFV
Finance app functions
Solves for the future value of an investment or loan
CalcFVNbPmt,IPYR,PV,PMTV,PPYR,CPYR,BEG
CalcNbPmt
CalcIPYR
CalcPMT
CalcPV
Triangle Solver app functions
Linear Solver app functions
Solve2x2
Solve3x3
ASAangle,side,angle
AASangle,angle,side
SASside,angle,side
SSAside,side,angle
DoSolve
Linear Explorer functions
SolveForYIntercept
Common app functions
Quadratic Explorer functions
SOLVEa, b, c
DELTAa, b, c
Function.CHECK1
Ctlg menu
UNCHECKDigit
Enter Sequence.UNCHECK2
Change Percent change from x to y. Returns 100*y-x/x
Percent of y. Returns x/100*y Example
List.Integer or Matrix.Integer
List1.*List2 or Matrix1.*Matrix2
Var=expression
3,4.*3,4,5,6 gives 3,8,15,24
A2q1,2,4,4,x,y returns x2+6*x*y+4*y2
A2qMatrix, Var1, Var2…
AbcuvPolyA, PolyB, PolyC, Var
Abcuvx2+2*x+1,x2-1,x+1 returns 1/2 -1/2
Append Appends an element to a list or vector
CanonicalformQuadraticExpr,Var
BasisMatrix
Canonicalform2*x2-12*x+1 gives 2*x-32-17
CatObject1, Object2,…
ColDim Returns the number of columns of a matrix
Complexrootx3+8, 0.01 returns
Companion Returns the companion matrix of a polynomial
Contains0,1,2,3,2 returns
ContainsList, Element or containsVector, Element
CopyVarVar1,Var2
CorrelationList or correlationMatrix
Returns
Enters the mathematical constant e Euler’s number
Eval Evaluates an expression
Eigenvals Returns the sequence of eigenvalues of a matrix
EvalfExpr,Integer
EvalcExpr
Evalf2/3 gives
Even1251 returns
ExprX+10 returns 100, if the variable X has the value
Expr Parses the string String into a number or expression
FMax-x2+2*x+1,x gives
FMaxExpr,Var
FMinExpr,Var
FMinx2-2*x+1,x gives
FunctiondiffFnc
FsolveExpr,Var,Guess or Interval,Method
Functiondiffsin gives x→cosx
GaussExpr,VectVar
Halftanhyp2expExprTrig
GramschmidtVector, Function
Halftanhyp2expsinx+sinhx returns
HamdistInteger1, Integer2
Icontent24x3+6x2-12x+18 gives
IcontentPoly,Var
Head1,2,3 gives
HeavisideReal
Inv Returns the inverse of an expression or matrix
Interval2center Returns the center of an interval
Jacobisymbol132,5 gives
JacobisymbolInteger1, Integer2
IPartReal or iPartList
IPart4.3 returns
Lin Returns an expression with the exponentials linearized
Logb Returns the logarithm of base b of a
Lname Returns a list of the variables in an expression
Mat2list Returns a list containing the elements of a matrix
Lvar Returns a list of variables used in an expression
Mean1,2,3,1,2,3 gives 7/3
MeanList1, List2 or meanMatrix
MedianList1, List2 or medianMatrix
Median1,2,3,5,10,4 gives
Modgcdx4-1,x-12 gives
ModgcdPoly1,Poly2
MRowExpr, Matrix, Integer
MultcconjugateExpr
NormalExpr
NDerivfx,x,h returns fx+h-fx-h*0.5/h
Normal2*x*2 gives 4*x
NormalizeVector or normalizeComplex
PIECEWISE⎪
PI Inserts π
Plotparamcost+i*sint, t=0..2*π plots the unit circle
PlotparamfVar+i*gVar, Var= Interval
PlotpolarExpr,Var=Interval
Plotpolarπ/2x, x=-π..π plots a partial spiral
Polecircle0, 1, line1+i, 2 returns point1/2,1/2
PoleCrcle,Line
POLYCOEFVector or POLYCOEFList
POLYCOEF-1, 1 returns 1, 0
PolynomialregressionList1, List2, Integer
PolygonscatterplotMatrix
Polynomialregression1, 2, 3, 4, 1, 4, 9, 16,3 returns 0 1 0
POLYROOTPoly or POLYROOTVector
Powerregression1, 2, 3, 4, 1, 4, 9, 16 returns 2
PowerregressionList1, List2
Powerpccircle0,1+i,3+i gives
Prepend1,2,3 gives 3,1,2
Purge Unassigns a variable name
Quote Returns an expression unevaluated
⎠ returns
RefMatrix
Reducedconicx2+2*x-2*y+1 returns
RemoveElement, Vector or removeElement, List
Remove6,1 2 6 7 returns 1 2
Restart Purges all the variables
Residue Returns the residue of an expression at a value
Example Gives
RowDim Returns the number of rows of a matrix
Signature Returns the signature of a permutation
Sqrt Returns the square root of an expression
Sto Stores a real or string in a variable
Transpose Returns a matrix transposed without conjugation
Sylvester Returns the Sylvester matrix of two polynomials
Type Returns the type of an expression e.g. list, string
Returns the square of an expression
When Used to introduce a conditional statement
Inserts the imaginary number
Creating your own functions
Expr
Function field, enter the function. eAA+fABAC
Variables
AaE
Working with Home variables
Result is written to history Multiply a by
AAxotwAS. Sq1o2 o3 E
Working with user variables Working with app variables
Example 3 You can also store objects in variables
More about the Vars menu
Qualifying variables
Home variables
Home variables are accessed by pressing aand Tapping
Function app variables
App variables
NumStart NumType NumStep NumZoom NumIndep
AAngle ADigits AComplex AFormat
Results variables
Geometry app variables
Spreadsheet app variables
Category Names Symbolic Plot
Solve app variables
ColWidth RowHeight
NumXStart
Advanced Graphing app variables
NumYStart NumType NumXStep NumXZoom NumYStep NumYZoom
Statistics 1Var app variables
MinVal
NbItem
MedVal
MaxVal
Statistics 2Var app variables
CoefDet
Corr
SCov
ΣCov
SerrY
Inference app variables
Contains the sum of the dependent values Y
CritVal1
CritScore
CritVal2
Prob
NumStart NumType NumStep NumZoom
Parametric app variables
Finance app variables
Polar app variables
Θmin Recenter
NumIndep NumType NumStart NumZoom NumStep
Triangle Solver app variables
Linear Solver app variables
Linear Explorer app variables
Quadratic Explorer app variables
Sequence app variables
Trig Explorer app variables
Category Names Modes
Units
Units and constants
Unit categories
Length Acceleration
Prefixes
Unit calculations
Units menu includes an entry that is not a unit
Palette of prefixes
+5 SF
MKSA8.175cm/s returns .08175m*s-1
Unit tools
UFACTOR100C,1A returns 100A*s
Physical constants
USIMPLIFY5kg*m2/s2 returns 5J
Value or measurement?
Avogadro, NA
List of constants
450
Create a list in the List Catalog
Lists
= or \
List Editor Buttons
List Editor
Keys
=or \
To insert an element
To edit a list
A list
Lists in Home view
Deleting lists
To delete a list
To createa list
Aj7
To store a list
To display a list
To display one
To send a list
List functions
Data on page 44 for instructions
2,3 returns 5,10,15
Sort
Make List
Menu format
Aajo
Reverse Concatenate Position Size
Aj5 E
Aj5E
Aj1E
Finding statistical values for lists
Aj1
Ad1E
Beginning on page 211, for the meaning of each statistic
Vectors
Matrices
Matrices
POLYROOT1,0,-1,0M1
Creating and storing matrices
Editor
Working with matrices
Matrix Editor
To create a matrix in the Matrix Editor
View
Matrices in Home
To store a matrix
To display a matrix
R1o2
Matrix arithmetic
To send a matrix
Matrixnamerow,column
HAQ1 +
E3 E
To multiply
Divide by a scalar
AQ1k5
AQ1sA
AQ1kQ
Q1 n AQ2
Solving systems of linear equations
2E3E Tap in cell R1, C3 E
1E1E Q1E
4EQ1
Commands
Matrix functions and commands
Sns AQ1E
Argument conventions
Matrix functions
TRN matrix
TRN ⎜
Rref
Rref matrix
3,2,3,4
IDENMATsize
0 JordanBlock7,3 returns 0 7 1 0 0
JordanBlockExpr,n
Hilbertn
Cos1 -sin1sin1 cos1
Rownorm ⎜
Specrad ⎜
Specnorm ⎜
Cond
Rank
37228… -0.37228…
EIGENVALmatrix
Eigenvv matrix
Eigenvv
Example CAS view
Choleskymatrix
Cholesky ⎜
IhermiteMtrxA
278
HessenbergMtrxA
IsmithMtrxA
Ismith ⎜
LSQ
LSQmatrix1, matrix2
P*A=L*U
LUmatrix
SCHURmatrix
QRmatrix A,var1,var2
Example Schur ⎛⎜ 1 2 ⎞⎟ returns
SVD ⎝
Cross 1 2 , 3 4 returns
4649… 0.3659…
DOT 1 2 , 3 4 returns
L2normVect
MaxnormVect or Mtrx
Examples
Maxnorm 1 2 3 -4 returns
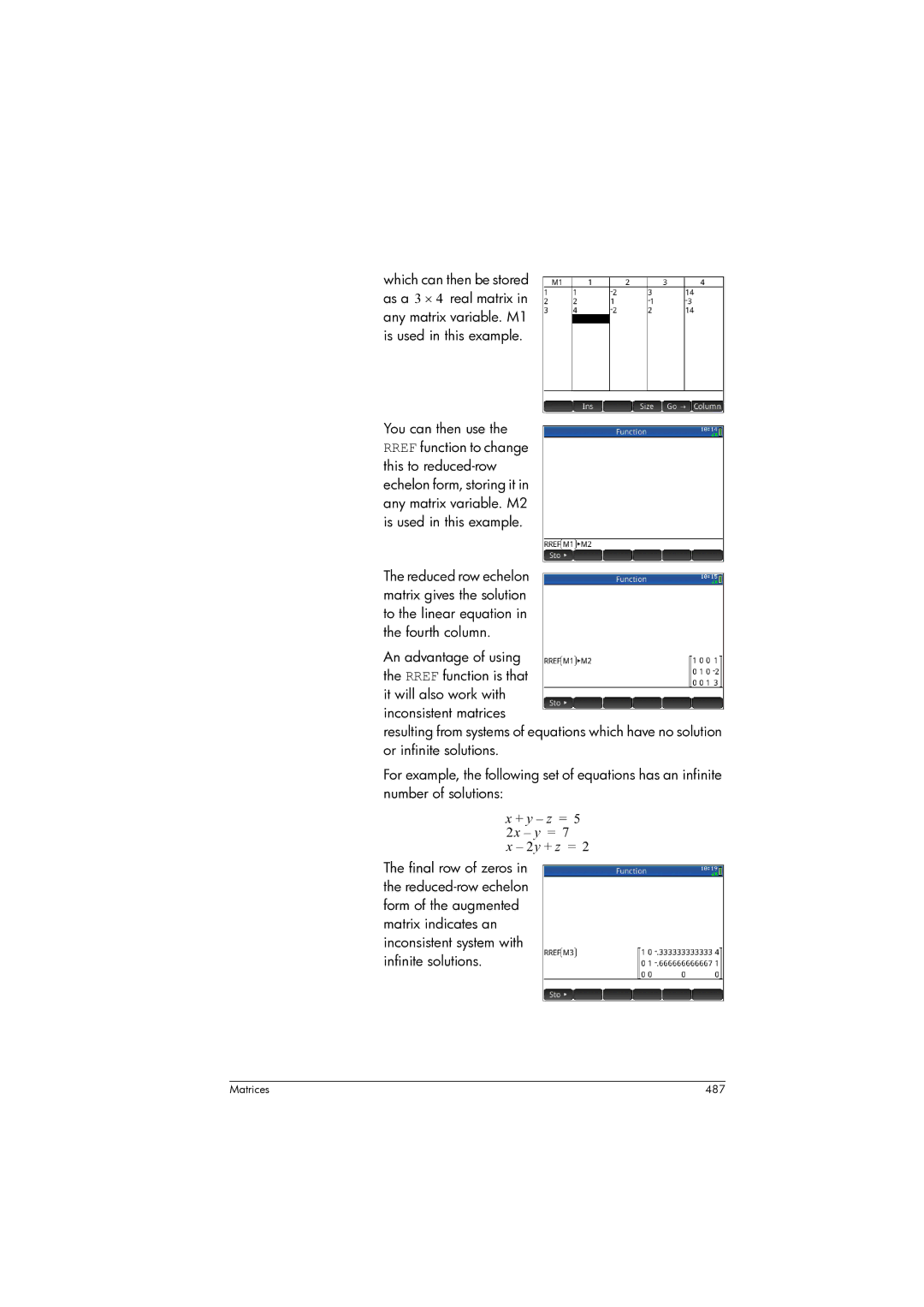
+ y z = 5 2x y = 2y + z =
488
Opens the selected note for
Features. See below
Editing
Begins a new note,
Rename renames the selected note
To create a note from the Notes Catalog
Open the Note Catalog
To create a note for an app
Are adding or editing a note
Keys
With lowercase locked, make next character uppercase
Make the next character upper-case
Text formatting
Mathematical
Inserting
Expressions
Sharing notes
Programming in HP PPL
HP Prime Programs Command Structure
Pixon xposition, yposition
Pixon xposition, yposition ,color
Program Structure Comments
Program Catalog
Export Myprogam Begin
END
Program Catalog buttons and keys
Open Program Catalog
=or S\
Myprogram
Creating a new program
Program Editor
Or S=and Checks the current program for errors
Strings Drawing Matrix App Functions Integer More
Press Jto return to the main menu
Begin and END
For N from 1 to 3 do
Tap Myprogram to expand the menu and select Myprogram
Run a Program
Multi-function
Debug a Program
Programs
Parameters
Program Catalog, select
Edit a program Copy a program or part of a program
510
To share a program
HP Prime programming language
Variables and visibility
Export Radius Export Getradius Begin Inputradius END
Programming in HP PPL 513
Program
Program Rolldie
Export Rolldien
Return 1+RANDINTN-1
Rolldie
L2roll+1 L2roll
ROLLDIEn
Return 1+RANDINTn-1 END
User Keyboard Customizing key presses
User mode
Begin Return 1+RANDINTN-1 END
Re-assigning keys
Internal name of keys and key states
Key names
KDiv
KAMath
App programs
Resets or Initializes an app
Using dedicated program functions Redefining the View menu
Starts an app
View text, function
Customizing an app
DiceSimulation
Tap Enter a name for the new app such as
Export SIDES,ROLLS Export DiceSimulation
Dicesimvars Rolldie
Begin END
View Roll Dice,ROLLMANY
Begin Repeat
Sides
SIDES= Floorsides If SIDES2 then
Until Sides =4 STARTVIEW7,1 END
STARTVIEW0,1 END
STARTVIEW1,1 END
Export ROLLS,SIDES Export Dicesimvars Begin
Sides END
Roll Dice
Program commands
Begin END Syntax Begin command1 command2… commandN END
Commands under the Tmplt menu Block
Branch
Export SQM1X Begin Return END
Loop
Default commands END
Case
MSGBOXMax of + max + factors for +result
Export Maxfactorsn Begin
MAXFACTORS100
Export Drawpattern Begin
END Wait
Rect
Export ISPERFECTn
Export Perfectnums Begin
+1 d END Return sum==n END
Export Sides Export Getsides Begin Repeat
INPUTSIDES,Die Sides,N = ,Enter num sides,2
Function
Variable
Export Syntax Export var1, var2, …, varn
Syntax Export FunctionName
Char Syntax CHARvector or CHARinteger
Commands under the Cmds menu Strings
666666666667
StringF1, when F1X Cosx = Cosx
String
INSTRINGvanilla,van returns Instring banana,na returns
Drawing
Ymax
Pixels and Cartesian
GETPIXPG, x, y
Getpix Syntax GETPIXG, x, y
Grobh Syntax Grobhg
Grobhpg
INVERTPG, x1, y1, x2, y2
Grobwpg
PIXOFFPG, x, y
PIXONPG, x, y ,color
Pixon Syntax PIXONG, x, y ,color
Wait END
Export BOX Begin Rect RECTP40,90,#0
Local sign K=2 A=4 sign=−1 Rect TEXTOUTPN=,0,0
Export Piseries Begin
Textoutppi APPROX=,0,30 Repeat
+sign*4/2*K-1 a
Until END
Sign*-1 sign K+1 K
Addcol Syntax ADDCOLmatrixname, vector, columnnumber
Addrow Syntax ADDROWmatrixname, vector, rownumber
Scale Syntax SCALEname, value, rownumber
Replace Syntax REPLACEname, start, object
Scaleadd Syntax Scaleadd name, value, row1, row2
SUB Syntax SUB name, start, end
App Functions
Bitand Syntax BITANDint1, int2, … intn
Commands
→R Syntax B→R#integerm
Bitsl Syntax BITSLint1 ,int2
Getbase Syntax GETBASE#integerm
Example GETBITS#22122 returns #20h or →B Syntax R→Binteger
Getbits Syntax GETBITS#integer
Setbits Syntax SETBITS#integerm ,bits
Choose Syntax CHOOSEvar, title, item1, item2,…,itemn
Taps Example EDITMATM1 edits matrix M1 Getkey Syntax Getkey
Editmat Syntax EDITMATmatrixvar
Export Sides Export Getsides
Input Syntax INPUTvar ,title, label, help, reset
Begin INPUTSIDES,D ie Sides,N = ,Enter num sides,2 END
Export Areacalc Begin
Msgbox Syntax MSGBOXexpression or string ,okcancel?
Programming in HP PPL 553
More
Executes the function or returns the variable using
CAS Syntax CAS.function or CAS.variable
Execon Syntax EXECON&expr, List1, list2,…
Example ITERATEX2, X, 2, 3 returns
Example →HMS54.8763 returns 5452′34.68″
EXECON&23+&1,1,5,16,4,5,6,7 returns 7,12
Variables and Programs
Programming in HP PPL 557
Plot view variables
App variables
Axes
Cursor
Hmin/Hmax
GridLines
Hwidth
Labels
Recenter S1mark-S5mark
Nmin/Nmax
SeqPlot
Θmin/θmax
Tstep
Θstep Polar Tmin/Tmax
Xtick Ytick Xmin/Xmax
Ymin/Ymax
Symbolic view variables
Xzoom
Yzoom
H1...H5
F0...F9
H1Type...H5Type
S1...S5
R0...R9
S1Type...S5Type
X0, Y0...X9,Y9
Type
U0...U9
C0...C9
Numeric view variables
D0...D9
NumIndep
NumXStep where n
NumStep where n
NumYStep where n
NumType-forAutomatic default NumType-forBuildYourOwn
NumYZoom where n
NumXZoom where n
Inference app variables
Alpha Conf
Mean2
Mean1
Mean1
Mean2
Pooled
Pooled-for not pooled default
Pooled-for pooled
Difference of two means or two proportions, sets
Variables
Finance app
CPYR
IPYR
NbPmt
NbPmt
PMTV
Triangle
Linear Solver app variables
Solver app
AngleA
SideC
AngleB
AngleC
Home
Settings
Date
HComplex
Time
Language
Base
Entry
Bits
Signed
Setup
Symbolic
AAngle
AComplex
AFormat
AFormat
580
Basic integer arithmetic
Default base
Binary, Octal, Decimal or Hex
Changing the default base
Mixed-base arithmetic
Examples of integer arithmetic
Integer manipulation
These are described in Integer, beginning on
Base functions
Glossary
Catalog
Record using the Program Editor
Matrix Two-dimensional array of real or
Vector One-dimensional array of real or
Symbolic, and Symbolic Setup
590
To reset
Troubleshooting
Calculator not responding
If the calculator does not turn on
Status messages
Operating limits
Name in the index to find its
Correct. Look up the function
Proper syntax
Apps, matrices, lists, notes, or
594
Federal Communications Commission notice
Product regulatory information
Modifications
Cables
596
European Union Regulatory Notice
598
Substances
Chemical
Parliament and the Council. a chemical information
600
Index
CAS 54
Menu 324-347 settings 30, 55 view
370-371
Functions 118-122, 348 variables
366-369
299-301
606
Samples 514-516, 524-527 structure
Zoom 88-94 points Polar app 70, 277-280 variables
215
Solve app 70, 259-266 functions 349 limitations 264 messages
App 109, 558-579 CAS
Types of 89-90