DSP_fft16x16
Implementation Notes
-Bank Conflicts: No bank conflicts occur.
-Interruptibility: The code is interruptible.
The routine uses log4(nx) − 1 stages of
|
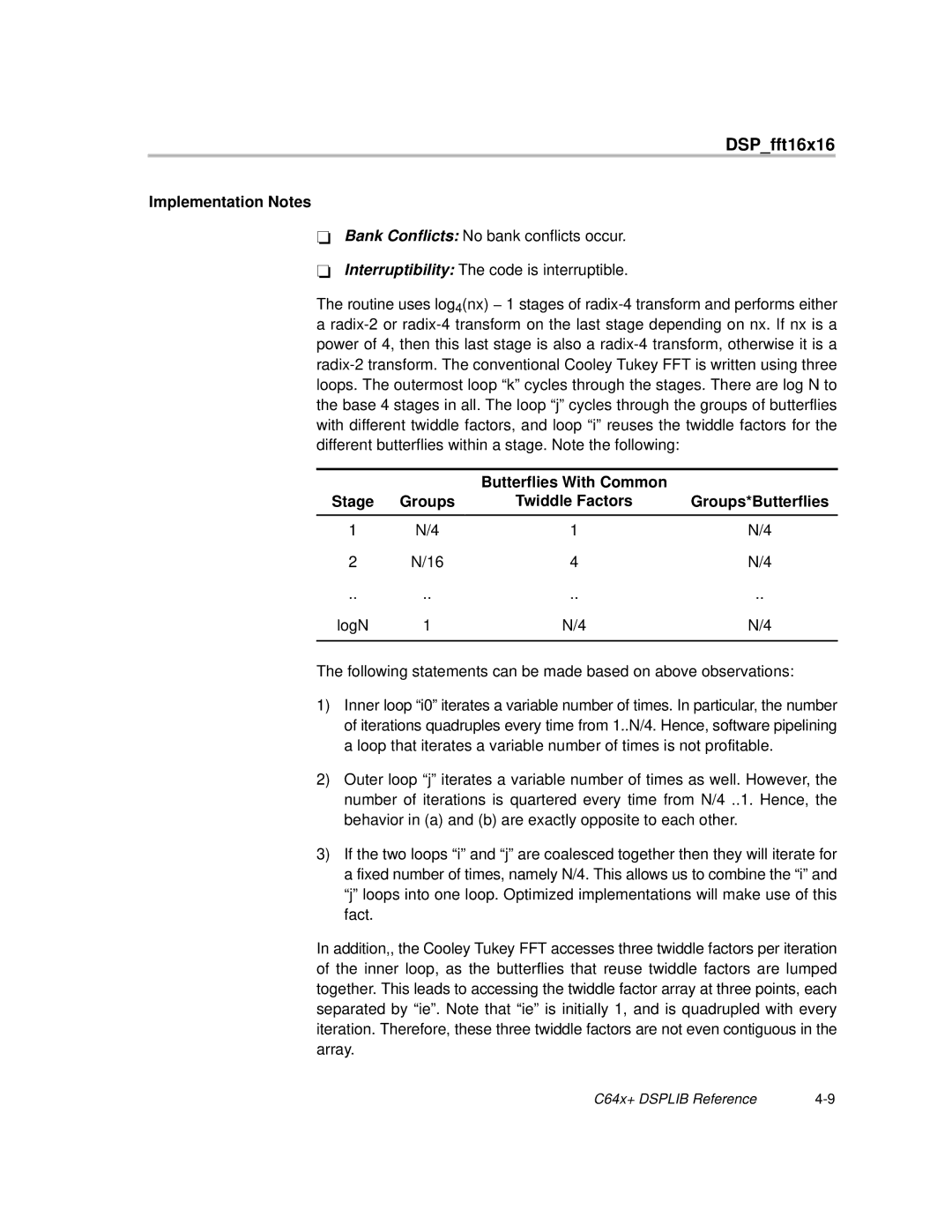
| Butterflies With Common |
|
Stage | Groups | Twiddle Factors | Groups*Butterflies |
|
|
|
|
1 | N/4 | 1 | N/4 |
2 | N/16 | 4 | N/4 |
.. | .. | .. | .. |
logN | 1 | N/4 | N/4 |
|
|
|
|
The following statements can be made based on above observations:
1)Inner loop “i0” iterates a variable number of times. In particular, the number of iterations quadruples every time from 1..N/4. Hence, software pipelining a loop that iterates a variable number of times is not profitable.
2)Outer loop “j” iterates a variable number of times as well. However, the number of iterations is quartered every time from N/4 ..1. Hence, the behavior in (a) and (b) are exactly opposite to each other.
3)If the two loops “i” and “j” are coalesced together then they will iterate for a fixed number of times, namely N/4. This allows us to combine the “i” and “j” loops into one loop. Optimized implementations will make use of this fact.
In addition,, the Cooley Tukey FFT accesses three twiddle factors per iteration of the inner loop, as the butterflies that reuse twiddle factors are lumped together. This leads to accessing the twiddle factor array at three points, each separated by “ie”. Note that “ie” is initially 1, and is quadrupled with every iteration. Therefore, these three twiddle factors are not even contiguous in the array.
C64x+ DSPLIB Reference |