Sharp EL9900 manual Slope and Intercept of Absolute Value Functions, If x ≥

EL-9900 Graphing Calculator

Slope and Intercept of Absolute Value Functions

The absolute value of a real number x is defined by the following:

x =	x if x ≥	0
	-xif x ≤	0

If n is a positive number, there are two solutions to the equation f (x) = n because there are exactly two numbers with the absolute value equal to n: n and -n.The existence of two distinct solutions is clear when the equation is solved graphically.

An absolute value function can be presented as y = ax - h + k. The graph moves as the changes of slope a, x-intercept h, and y-intercept k.

Example

Consider various absolute value functions and check the relation between the graphs and the values of coefficients.

1. Graph y = x

2. Graph y = x -1 and y = x-1 using Rapid Graph feature.

Before There may be differences in the results of calculations and graph plotting depending on the setting. Starting Return all settings to the default value and delete all data.

Set the zoom to the decimal window: ZOOM A ( ENTER 2nd F ) 7

Step & Key Operation Display Notes

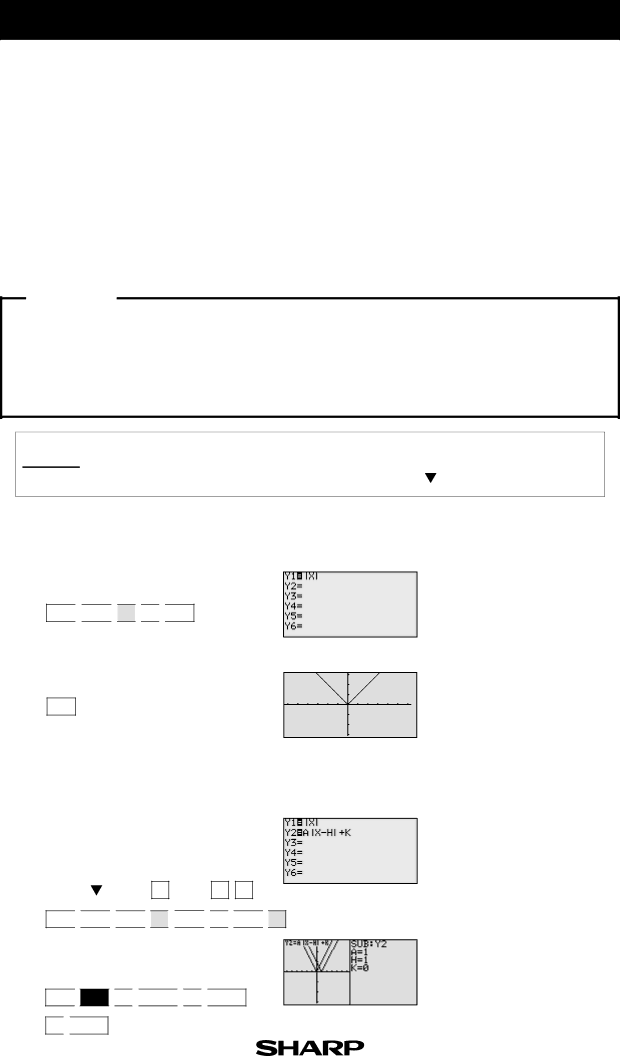
1-1Enter the function y =x for Y1.

Y= MATH B 1 X//T/n

1-2View the graph.

GRAPH

Notice that the domain of f(x)

=x is the set of all real num- bers and the range is the set of non-negative real numbers. Notice also that the slope of the

graph is 1 in the range of X > 0 and -1 in the range of X ≤ 0.

2-1

2-2

10-1

Enter the standard form of an abso- lute value function for Y2 using the Rapid Graph feature.

Y= ALPHA A MATH B 1

X//T/n — ALPHA H + ALPHA K

Substitute the coefficients to graph y = x - 1.

2nd F SUB 1 ENTER 1 ENTER

0 ENTER