Sharp EL9900 manual Graphing Circles, Graph x 2 2x + y 2 + 4y =, 2x + y+22 =, +22 = 6 -x 2 +

EL-9900 Graphing Calculator

Graphing Circles

The standard equation of a circle of radius r that is centered at a point (h, k) is (x - h) 2 + (y - k) 2 = r 2. In order to put an equation in standard form so that you can graph in rectangular mode, it is necessary to solve the equation for y. You therefore need to use the process of completing the square.

Example

Graph the circles in rectangular mode. Solve the equation for y to put it in the standard form.

1. Graph x 2 + y 2 = 4.

2. Graph x 2 - 2x + y 2 + 4y = 2.

Before There may be differences in the results of calculations and graph plotting depending on the setting. Starting Return all settings to the default value and delete all data.

Set the zoom to the decimal window:

ZOOM A

(

ENTER

ALPHA

)

7

Step & Key Operation Display Notes

1-1

1-2

2-1

Solve the equation for y.

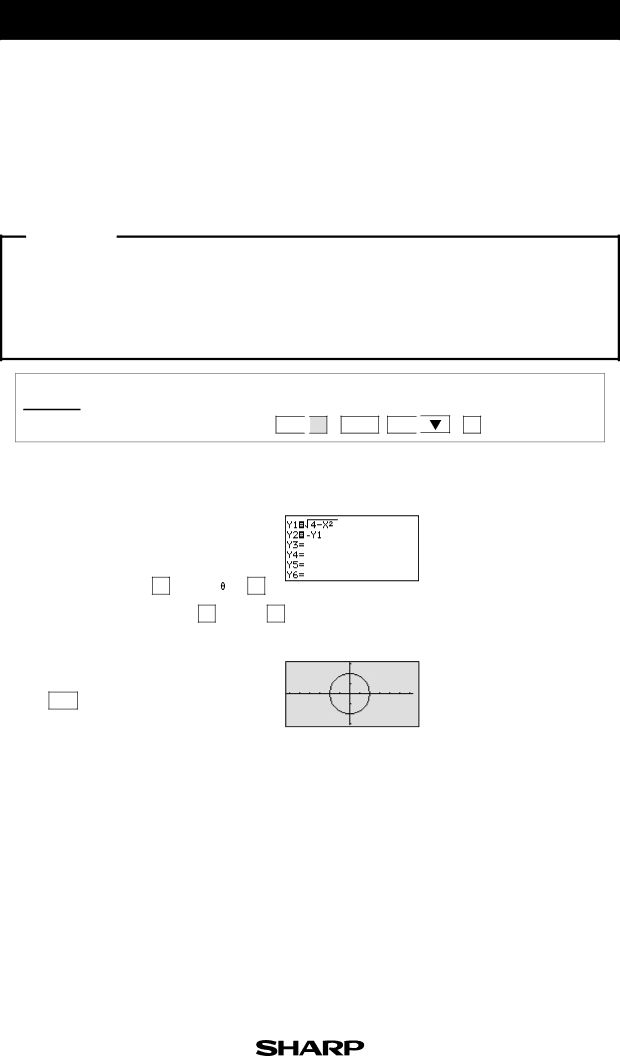
y 2 = 4 - x 2

Enter y = √

4 - x 2

for Y1 (the top

y = –+√

4 - x 2

half). Enter y = -√

4 - x 2

for Y2.

x2

Y=

2nd F

√

4

—

X/ /T/n

ENTER

( )

2nd F

VARS

A

ENTER

1

-

View the graph.

This is a circle of radius r ,

centered at the origin.

GRAPH

Solve the equation for y,	x 2 - 2x + y 2 + 4y = 2				Place all variable terms on the
					left and the constant term on
completing the square.
					the right-hand side of the
					equation.
	x 2 - 2 x+y 2 + 4 y+ 4 = 2 + 4				Complete the square on the
					y-term.
	x 2 - 2x + (y+2)2 = 6				Express the terms in y as a
					perfect square.
	(y+2)2 = 6 -x 2 + 2x				Leave only the term involving
					y on the left hand side.
	y+2 = ± √
			6-x 2+2x		Take the square root of both
					sides.
	y = ± √			-2
		6-x 2+2x			Solve for y.

12-2