Sharp EL9900 manual Solving Absolute Value Equations, Solve an absolute value equation 5 4x =

EL-9900 Graphing Calculator

Solving Absolute Value Equations

The absolute value of a real number x is defined by the following:

x =	x if x ≥	0
	-xif x ≤	0

If n is a positive number, there are two solutions to the equation f (x) = n because there are exactly two numbers with the absolute value equal to n: n and -n.The existence of two distinct solutions is clear when the equation is solved graphically.

Example

Solve an absolute value equation 5 - 4x = 6

	Before	There may be differences in the results of calculations and graph plotting depending on the setting.
Starting		Return all settings to the default value and delete all data.
	Step & Key Operation		Display	Notes

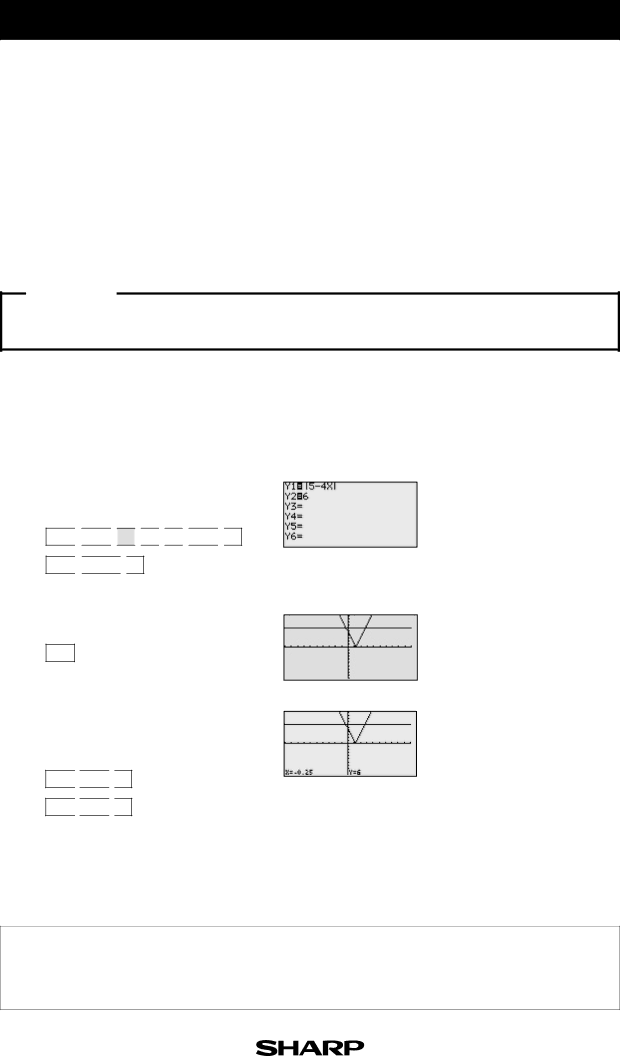
1Enter y = 5 - 4x for Y1. Enter y = 6 for Y2.

Y= MATH B 1 5 — 4

X//T/n ENTER 6

2View the graph.

GRAPH

3Find the points of intersection of the two graphs and solve.

2nd F CALC 2

2nd F CALC 2

There are two points of in- tersection of the absolute value graph and the hori- zontal line y = 6.

The solution to the equation 5 - 4x= 6 consists of the two values -0.25 and 2.75. Note that although it is not as intu- itively obvious, the solution could also be obtained by finding the x-intercepts of the function y = 5x - 4 - 6.

The EL-9900 shows absolute values with , just as written on paper, by using the Equation editor. The graphing feature of the calculator shows the solution of the absolute value function visually.

10-2