Sharp EL9900 manual 1Change the equation in Y2 to y = x 2+2

EL-9900 Graphing Calculator

Step & Key Operation Display Notes

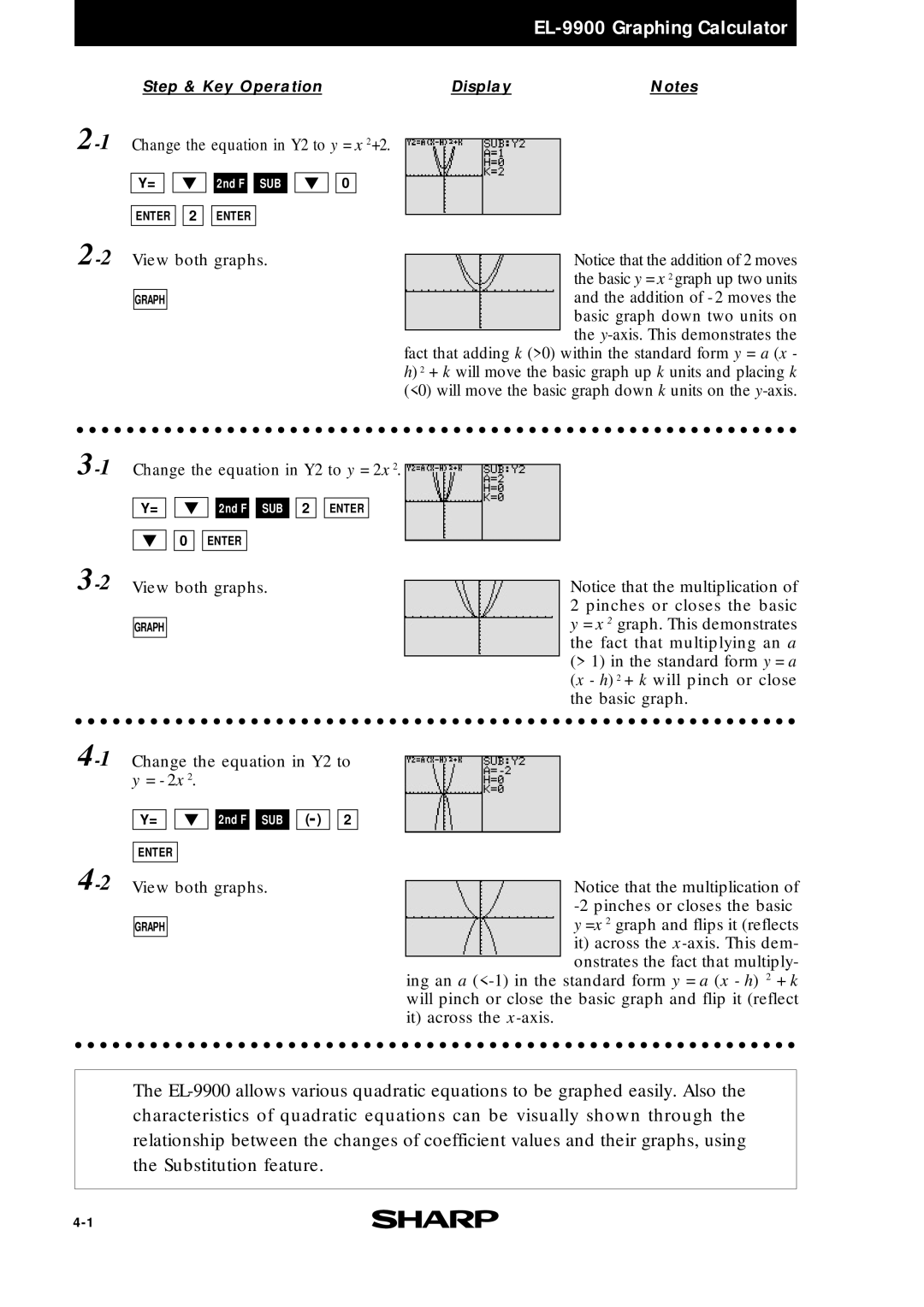
2-1Change the equation in Y2 to y = x 2+2.

Y= 2nd F SUB 0

ENTER 2 ENTER

2-2View both graphs.

GRAPH

Notice that the addition of 2 moves the basic y = x 2 graph up two units and the addition of - 2 moves the basic graph down two units on the y-axis. This demonstrates the

fact that adding k (>0) within the standard form y = a (x - h) 2 + k will move the basic graph up k units and placing k (<0) will move the basic graph down k units on the y-axis.

3-1Change the equation in Y2 to y = 2x 2.

Y=			2nd F	SUB	2	ENTER
	0	ENTER

3-2View both graphs.

GRAPH

Notice that the multiplication of 2 pinches or closes the basic y = x 2 graph. This demonstrates the fact that multiplying an a (> 1) in the standard form y = a (x - h) 2 + k will pinch or close the basic graph.

4-1Change the equation in Y2 to y = - 2x 2.

Y=	2nd F	SUB	(	-	2
				)

ENTER

4-2View both graphs.

GRAPH

Notice that the multiplication of -2 pinches or closes the basic y =x 2 graph and flips it (reflects it) across the x-axis. This dem- onstrates the fact that multiply-

ing an a (<-1) in the standard form y = a (x - h) 2 + k will pinch or close the basic graph and flip it (reflect it) across the x-axis.

The EL-9900 allows various quadratic equations to be graphed easily. Also the characteristics of quadratic equations can be visually shown through the relationship between the changes of coefficient values and their graphs, using the Substitution feature.

4-1