Vs = Vx 2 + Vy | Galil DMC-13X8 guide

Vs = Vx 2 + Vy 2

The vector distance is the integral of Vs, or the total distance traveled along the path. To illustrate this further, suppose that a string was placed along the path in the X-Y plane. The length of that string represents the distance traveled by the vector motion.

The vector velocity is specified independently of the path to allow continuous motion. The path is specified as a collection of segments. For the purpose of specifying the path, define a special X-Y coordinate system whose origin is the starting point of the sequence. Each linear segment is specified by the X-Y coordinate of the final point expressed in units of resolution, and each circular arc is defined by the arc radius, the starting angle, and the angular width of the arc. The zero angle corresponds to the positive direction of the X-axis and the CCW direction of rotation is positive. Angles are expressed in degrees, and the resolution is 1/256th of a degree. For example, the path shown in Fig. 12.2 is specified by the instructions:

	VP	0,10000
	CR	10000, 180, -90
	VP	20000, 20000
	Y
20000		C	D
10000	B
	A		X
		10000	20000
Figure 12.2 - X-Y Motion Path

The first line describes the straight line vector segment between points A and B. The next segment is a circular arc, which starts at an angle of 180° and traverses -90°. Finally, the third line describes the linear segment between points C and D. Note that the total length of the motion consists of the segments:

A-B Linear

10000 units

USER MANUAL

Appendices • 199

Image 199

Galil DMC-13X8 user manual Vs = Vx 2 + Vy

Contents

DMC-13X8 Using This Manual Contents Connecting Hardware Programming Motion Hardware & Software Protection 149 ZOH DAC Index 207 Overview of Motor Types IntroductionOverview Brushless Servo Motor with Sinusoidal Commutation Standard Servo Motor with +/- 10 Volt Command SignalStepper Motor with Step and Direction Signals DMC-13X8 Functional Elements General I/O Microcomputer SectionMotor Interface Communication Motor System ElementsAmplifier Driver Encoder Watch Dog Timer This page Left Blank Intentionally Getting Started DMC-13X8 Motion Controller JP9 Elements You Need Sinusoidal Commutation Installing the DMC-13X8Determine Overall Motor Configuration Standard Servo Motor Operation Install Jumpers on the DMC-13X8 Optional Motor Off Jumpers Install the DMC-13X8 in the VME HostEstablish Communication with the Galil controller Determine the Axes to be Used for Sinusoidal Commutation Baxz Make Connections to Amplifier and Encoder Getting Started Check the Polarity of the Feedback Loop Connect Standard Servo Motors BGX CR Inverting the Loop PolarityTTX CR DC Power Supply DC Brush Connect Sinusoidal Commutation Motors If Hall Sensors are Not Available If Hall Sensors are Available BCX SHXBGX AMX Tune the Servo System Connect Step Motors InstructionInterpretation Design ExamplesExample 1 System Set-up TE X CR Example 5 Position Interrogation Example 2 Profiled MoveExample 3 Multiple Axes Example 4 Independent Moves Example 7 Velocity Control Example 6 Absolute Position Example 9 Interrogation Example 10 Operation in the Buffer ModeExample 11 Using the On-Board Editor Example 8 Operation Under Torque Limit Example 13 Motion Programs with Trippoints Example 12 Motion Programs with Loops Example 15 Linear Interpolation Example 14 Control VariablesExample 16 Circular Interpolation 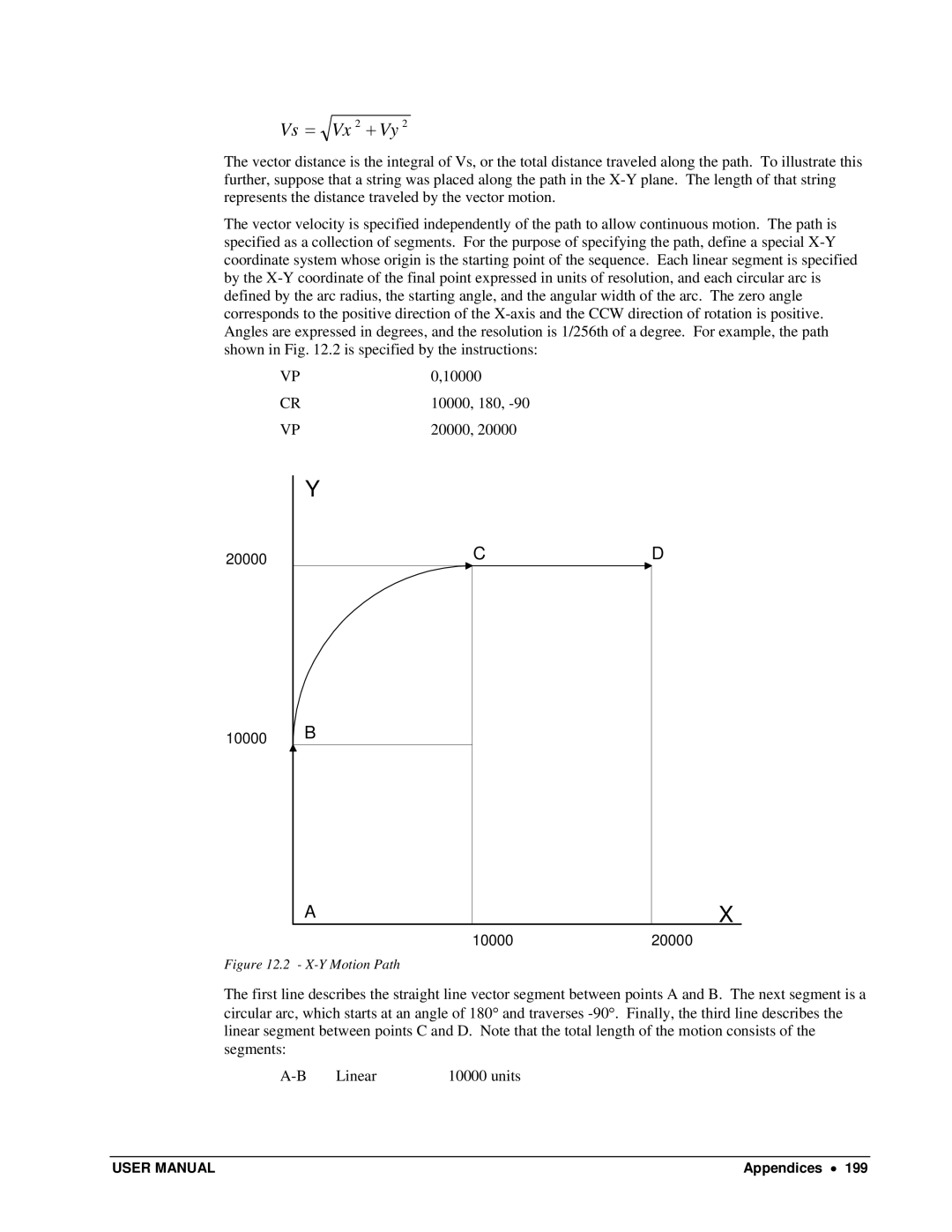Motion Path for Example VM XY Overview Using Optoisolated InputsLimit Switch Input Connecting Hardware Abort Input Home Switch Input Group Controllers with 1- 4 Axes Common Signal Wiring the Optoisolated InputsUncommitted Digital Inputs Optoisolated Inputs Using an Isolated Power Supply Amplifier Interface Analog InputsBypassing the Opto-Isolation ICM-1900/2900 TTL Inputs TTL Outputs This page Left Blank Intentionally Register Description Address Read/Write Communication with ControllerCommunication Registers AM5 AM4 AM3 AM2 AM1 AM0 Advanced Communication Techniques Simplified Communication Procedure Communication with Controller Secondary Fifo channel Polling Mode Read ProcedurePolling Fifo Addr Type Overview of Secondary Fifo ProcedureDMA / Secondary Fifo Memory Map Operation Register address Value Error code BIT Axis Switch Information 1 ByteGeneral Status Information 1 Byte Axis Status Information 2 Byte Configuring Interrupts Setting up InterruptsInterrupts Bit number n Input Bit Number m Condition Hex Data Condition Servicing InterruptsExample Interrupts BGY UI1 Controller Response to Data Command Basics Command Syntax Ascii BG TW Coordinated Motion with more than 1 axisBG Xyzw BG S Datafields Format Command Syntax BinaryBinary Command Format Header Format LE, VE Binary command tableCommand Example Interrogating the Controller Interrogation Commands =TPX Summary of Interrogation CommandsInterrogating Current Commanded Values Operands Command Summary This page Left Blank Intentionally Programming Motion Example Application Mode of Motion Commands Independent Axis Positioning Example Multiple Move Sequence Command Summary Independent AxisOperand Summary Independent Axis Example Absolute Position Movement Axis velocity profile Velocity COUNTS/SEC Independent Jogging Command Summary JoggingExample Jog in X only Specifying Linear Segments Linear Interpolation ModeExample Joystick Jogging #LMOVE Additional CommandsAn Example of Linear Interpolation Motion Specifying Vector Speed for Each Segment LM? Command Summary Linear InterpolationChanging Feedrate #ALT Example Linear Move Operand Summary Linear InterpolationLM ZW #LOAD Example Multiple MovesCOUNT=0 Specifying the Coordinate Plane Vector Mode Linear and Circular Interpolation MotionSpecifying Vector Segments Additional commands Trippoints Compensating for Differences in Encoder ResolutionTangent Motion Operand Summary Coordinated Motion Sequence Command Summary Coordinated Motion Sequence Required Path Electronic Gearing Example Electronic Gearing Command Summary Electronic GearingCommand Description Example Simple Master Slave Electronic Cam Example Gantry Mode EAp where p = X,Y,Z,W Is the selected master axis Programming Motion 3000 2250 1500 2000 4000 6000 Master Instruction Interpretation Command Summary Electronic CAM Example Electronic CAM Operand Summary Electronic CAMOperand Description Specifying Contour Segments Contour Mode DT0CD0 CMX Generating an Array An Example Command Summary Contour ModeOperand Summary Contour Mode General Velocity Profiles POSC=V4 Contour Mode ExampleInstruction Interpretation #POINTS Record and Playback Example Teach Record and Play-Back AC, DC, JG, SP, PR, PA, BG, IT, GA, VM, VP, CR, ST, DP, RP Virtual AxisBGN Stepper Motor Smoothing Monitoring Generated Pulses vs Commanded PulsesStepper Motor Operation Specifying Stepper Motor Operation Motion Complete Trippoint Using an Encoder with Stepper Motors Command Summary Stepper Motor Operation Stepper Position Maintenance Mode SPMOperand Summary Stepper Motor Operation Example SPM Mode Setup Error LimitCorrection Half-Stepping Drive, X axis Example Error Correction #MOTION #LOOP Example Friction Correction = Main Encoder Second Encoder Using the CE CommandAdditional Commands for the Auxiliary Encoder Dual Loop Auxiliary Encoder #DUALOOP Backlash CompensationContinuous Dual Loop Example Sampled Dual Loop Example Motion Smoothing Using the IT and VT CommandsExample Smoothing Trapezoidal velocity and smooth velocity profiles Using the KS Command Step Motor Smoothing Homing Motion intervals in the Home sequence FE Xyzw FI Xyzw HM Xyzw SC Xyzw TS Xyzw Command Summary Homing OperationHigh Speed Position Capture The Latch Function Operand Summary Homing Operation AL Y Fast Update Rate Mode This page Left Blank Intentionally ED #BEGIN Using the DMC-13X8 Editor to Enter ProgramsApplication Programming Program Format Edit Mode CommandsReturn #BEGIN1 Using Labels in ProgramsSpecial Labels #BEGIN #SQUARE No Bottom Line Using the command, noExecuting Programs Multitasking Commenting Programs Debugging Programs Trace Commands Operands Error Code CommandStop Code Command RAM Memory Interrogation Commands Event Triggers & Trippoints Program Flow Commands Function DMC-13X8 and DMC-13X8 Event Triggers Event Trigger Repetitive Position Trigger Event Trigger ExamplesEvent Trigger Multiple Move Sequence Event Trigger Set Output after Distance Event Trigger Start Motion on Input Event Trigger Set output when At speedEvent Trigger Change Speed along Vector Path Conditional Jumps Define Output Waveform Using ATEvent Trigger Multiple Move with Wait Multiple Conditional Statements Command Format JP and JSLogical operators Conditional Statements Using the if and Endif Commands Using If, Else, and Endif CommandsUsing the JP Command Example Using JP command Nesting if Conditional Statements Using the Else CommandCommand Format IF, Else and Endif Example using IF, Else and Endif Stack Manipulation SubroutinesAuto-Start Routine Subroutine Description Example Limit SwitchExample Position Error Automatic Subroutines for Monitoring Conditions Example Input Interrupt Example Motion Complete Timeout Example Command Error w/Multitasking Example Command ErrorOperand Function Operator Function Mathematical and Functional ExpressionsMathematical Operators Bit-Wise Operators LEN1=FLEN&$00FF FunctionsENTER,LENS6 FLEN=@FRACLEN Reallongname VariablesProgrammable Variables Posx POS1 Speedz Displaying the value of variables at the terminal Example Using Variables for JoystickAssigning Values to Variables Assigning Variable Values to Controller Parameters Examples of Keywords OperandsSpecial Operands Keywords Examples of Internal Variables Assignment of Array Entries Using a Variable to Address Array ElementsArrays Defining Arrays Automatic Data Capture into Arrays Command Summary Automatic Data CaptureUploading and Downloading Arrays to On Board Memory Data Type Description Data Types for RecordingOperand Summary Automatic Data Capture Example Recording into An Array An Example for Inputting Numeric Data Input of Data Numeric and StringDeallocating Array Space Input of Data Formatting Messages Output of Data Numeric and StringSending Messages Inputting String Variables Displaying Variables and Arrays Using the MG Command to Configure TerminalsSummary of Message Functions BL ? LE ? DE ? PA ? DP ? PR ? EM ? LZ0 Local Formatting of Response of Interrogation CommandsFormatting Variables and Array Elements Local Formatting of Variables Converting to User Units Hardware I/ODigital Outputs Instruction Function Digital Inputs Input Interrupt Function Example Start Motion on SwitchExamples Input Interrupt Example Position Follower Point-to-Point Analog InputsExample Position Follower Continuous Move Example Applications Wire CutterJP #A Table Controller Motor Velocity and the Associated Input/Output signals BGS AMS BGZAMZ BGZ AMZ Speed Control by Joystick DP0 Position Control by JoystickBacklash Compensation by Sampled Dual-Loop JG VEL JP #B PR ER LINPOS=0LIN POS = DEX ER=1000-LINPOS-TEX This page Left Blank Intentionally Output Protection Lines Hardware ProtectionHardware & Software Protection Programmable Position Limits Signal or Function State if Error OccursSoftware Protection Input Protection Lines #AJP #AEN Off-On-ErrorAutomatic Error Routine Limit Switch Routine Stxamx V2=LRXJP#END #LF Remedy InstallationSymptom Diagnosis Cause Troubleshooting Communication Operation Stability This page Left Blank Intentionally Theory of Operation Theory of Operation Level Velocity and Position Profiles Operation of Closed-Loop Systems System Modeling Voltage Drive Motor-Amplifier Velocity Loop Current Drive Voltage Source Digital Filter DAC ZOH System Analysis Ms = P/I = Kt/Js2 = 500/s2 rad/A Amp Ka = 4 Amp/V Analytical Method System Design and Compensation Kd = 10/32768 = Encoder Kf = 4N/2π = Theory of Operation KP, KD, KI, PL Equivalent Filter FormPID, T Input/Output Electrical SpecificationsServo Control Stepper Control Power Performance Specifications J1 DMC-13X8 A-D Axes Main J5-DMC-13X8 A-D Axes Connectors for DMC-13X8 Main BoardPIN High Density Auxiliary Encoders 26-PIN IDC PWM/STEP OUT Pin-Out Description for DMC-13X8 Accessories and Options Terminal # Label Description ICM-1900 Interconnect Module ABY ErrorReset +ABY Ylatch RlsxFlsx Xlatch +MBZ INY+MAZ MAZ ICM-1900 Drawing AMP-19X0 Mating Power Amplifiers OUT PWR ICM-2900 Interconnect ModuleOUT GND ANALOG7 ANA GNDANALOG5 ANALOG6 ANALOG4 ANALOG1ANALOG2 ANALOG3 Extended I/O of the DMC-13X8 Controller Opto-Isolated Outputs ICM-1900 / ICM-2900 -Opto optionStandard Opto-isolation and High Current Opto-isolation BIT I/O Block Binary Representation Decimal Value for Block Configuring the I/O of the DMC-13X8Accessing extended I/O Saving the State of the Outputs in Non-Volatile Memory BIT # Connector DescriptionPIN Signal Block BIT @INn GND @OUTn Description IOM-1964 Opto-Isolation Module for Extended I/O Controllers Overview Configuring Hardware Banks For example, here is the layout of bank Sinking Sourcing Input Circuit High Power Digital Outputs Internal Pullup Standard Digital Outputs Standard Digital Outputs Electrical SpecificationsHigh Power Digital Outputs Digital Inputs Screw Terminal Listing Relevant DMC CommandsTerminal Label Description Appendices Coordinated Motion Mathematical Analysis Vs = Vx 2 + Vy Velocity Tt = VSD + Ta = 0.407s DMC-13X8 DMC-13X8/DMC-1300 ComparisonList of Other Publications Benefit WHO should Attend Training Seminars Galil Motion Control Contacting Us Warranty 206 Poserr LimswiIndex Address ... Error! Not a valid bookmark in entry on Interrupt...Error! Not a valid bookmark in entry on Stop