More about Integration | HP 35s Scientific instruction

f (x)

x

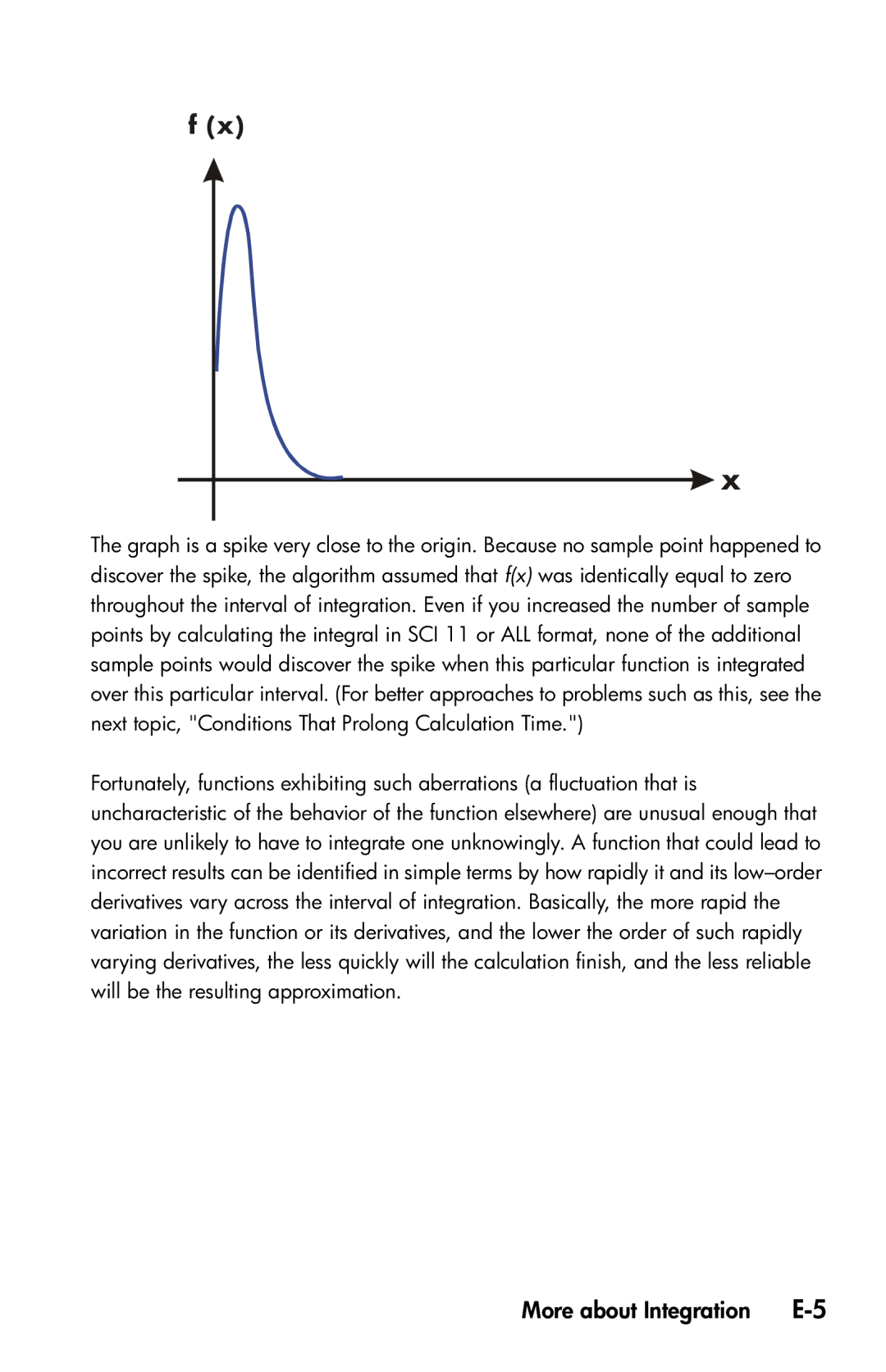
The graph is a spike very close to the origin. Because no sample point happened to discover the spike, the algorithm assumed that f(x) was identically equal to zero throughout the interval of integration. Even if you increased the number of sample points by calculating the integral in SCI 11 or ALL format, none of the additional sample points would discover the spike when this particular function is integrated over this particular interval. (For better approaches to problems such as this, see the next topic, "Conditions That Prolong Calculation Time.")

Fortunately, functions exhibiting such aberrations (a fluctuation that is uncharacteristic of the behavior of the function elsewhere) are unusual enough that you are unlikely to have to integrate one unknowingly. A function that could lead to incorrect results can be identified in simple terms by how rapidly it and its low–order derivatives vary across the interval of integration. Basically, the more rapid the variation in the function or its derivatives, and the lower the order of such rapidly varying derivatives, the less quickly will the calculation finish, and the less reliable will be the resulting approximation.

More about Integration

E-5

Image 341

HP 35s Scientific manual More about Integration

Contents

Users guide HP 35s scientific calculator Printing History Contents Storing Data into Variables Viewing a Variable ContentsRPN The Automatic Memory Stack Quotient and Remainder of Division Real-Number FunctionsTrigonometry Entering π Hyperbolic Functions Entering and Evaluating Equations Fractions Integrating Equations Solving EquationsOperations with Complex Numbers Vector Arithmetic 10-1 Statistical Operations 12-1 Base Conversions and Arithmetic and Logic 11-110-7 Creating Vectors from Variables or Registers 10-8 Simple Programming 13-1 Part 2. Programming Programming Techniques 14-1 Part 3. Appendixes and Reference Support, Batteries, and ServiceSolving and Integrating Programs 15-1 Statistics Programs 16-1 More about Solving User Memory and the StackALG Summary More about Integration Round-Off ErrorMessages Operation Index How the Integral Is Evaluated Contents Part Page Getting Started Adjusting Display ContrastImportant Preliminaries Turning the Calculator On and Off 2Getting Started Highlights of the Keyboard and DisplayShifted Keys Cursor Keys Alpha KeysFunction Key Left-shifted function Right-shifted Letter for alphabetic Backspacing and Clearing  Clear or CancelKeys for Clearing 4Getting Started Clear menu       Key Description ˆ ˆ    Using MenusHP 35s Menus Chapter Name 6Getting Started Other functions Programming Instructions or  Exiting Menus 8  RPN and ALG ModesKeys Display KeysDisplay 10Getting Started RPN mode ALG mode Undo key First Line Second Line Display and AnnunciatorsAnnunciators 12Getting Started EQN HP 35s Annunciators Meaning Chapter 14Getting Started Exponents of Ten Keying in NumbersMaking Numbers Negative 16Getting Started z Range of Numbers and Overflow Understanding Entry Cursor  18Getting Started Performing Arithmetic CalculationsSingle Argument or Unary Operations Key RPN,RPN Program ALG, Equation, ALG Program Two Argument or Binary Operations   Õ Key RPN, RPN Program ALG, Equation, ALG Program Controlling the Display Format 22Getting Started Periods and Commas in Numbers   8 Complex number display format  ,  , 8 24Getting Started 8   SHOWing Full 12-Digit Precision8×  26Getting Started FractionsEntering Fractions  Messages É  28Getting Started Calculator MemoryChecking Available Memory Clearing All of Memory 30Getting Started RPN The Automatic Memory Stack RPN The Automatic Memory StackWhat the Stack Is 2RPN The Automatic Memory Stack Reviewing the Stack X and Y-Registers are in the DisplayClearing the X-Register 4RPN The Automatic Memory Stack Exchanging the X- and Y-Registers in the StackPress  Arithmetic How the Stack Does It 6RPN The Automatic Memory Stack How Enter Works Filling the stack with a constant How to Clear the Stack 8RPN The Automatic Memory Stack Last X Register Correcting Mistakes with Last  Ù Reusing Numbers with Last    Work from the Parentheses Out Chain Calculations in RPN Mode     Order of Calculation Exercises       More Exercises       18RPN The Automatic Memory Stack Storing Data into Variables AKeys DisplayDescription 2Storing Data into Variables Storing and Recalling NumbersPress letter-key  Press letter-key    AG  Viewing a Variable Using the MEM CatalogVAR catalog 4Storing Data into Variables D E C Storage Arithmetic Arithmetic with Stored Variables6Storing Data into Variables Storage arithmetic uses , , , or  Recall Arithmetic  D Exchanging x with Any VariableD E A Variables I and J 10Storing Data into Variables Real-Number Functions Exponential and Logarithmic Functions Quotient and Remainder of Division Power Functions    Entering π Trigonometry Trigonometric Functions Setting the Angular ModeOption Description Annunciator 4Real-Number Functions   Percentage Functions Hyperbolic Functions     8Real-Number Functions Physics ConstantsConst Menu Items Description Value Items Description Value 10Real-Number Functions Conversion FunctionsRectangular/Polar Conversions 30o 12Real-Number Functions 86  Time ConversionsAngle Conversions Unit Conversions Factorial Probability FunctionsGamma Probability 16Real-Number Functions  Integer part Parts of NumbersFractional part Absolute value 18Real-Number Functions To calculatePressDisplay   FractionsEntering Fractions 2Fractions Fractions in the DisplayDisplay Rules Entered Value Internal Value Displayed Fraction Accuracy Indicators 4Fractions Setting the Maximum DenominatorChanging the Fraction Display  6Fractions Choosing a Fraction Format To Get This Fraction Format Change These Flags   j Examples of Fraction Displays Rounding Fractions Fractions in Equations 10Fractions Fractions in Programs How You Can Use Equations Entering and Evaluating EquationsEntering and Evaluating Equations = .25 π d2 l Value      D 2Entering and Evaluating Equations Key Operation Summary of Equation Operations 4Entering and Evaluating Equations Entering Equations into the Equation ListVariables in Equations Functions in Equations Numbers in Equations Parentheses in Equations Displaying and Selecting Equations   Ö  8Entering and Evaluating Equations Editing and Clearing Equations Types of Equations 10Entering and Evaluating Equations Evaluating Equations Type of Equation Result for  Result for  Using Enter for Evaluation 12Entering and Evaluating Equations Using XEQ for Evaluation       Responding to Equation Prompts 14Entering and Evaluating Equations Syntax of EquationsOperator Precedence Equations Meaning Order Operation Example Σxy Equation Functions16Entering and Evaluating Equations Perimeter = a + b + h sin1θ + sin1φ RPN Operation Equation function Area = 18Entering and Evaluating Equations  Õ Syntax ErrorsVerifying Equations 20Entering and Evaluating Equations Solving an Equation Solving EquationsSolving Equations Markup ⋅ Cost = Price = v0 t + 1/2 g t 2Solving Equations  G    P      P    Solving built-in Equation 6Solving Equations  Understanding and Controlling SolveVerifying the Result 8Solving Equations Interrupting a Solve CalculationChoosing Initial Guesses for Solve Solving Equations = 40 H ⋅ 20 H ⋅ 4 ⋅ H 10Solving EquationsType in the equation Equation H  value 4H   12Solving Equations For More Information Integrating Equations Integrating Equations 2Integrating Equations Integrating Equations FN   J0 x = π 0 cosx sin t dt 4Integrating Equations = t X SinxX  Specifying Accuracy Accuracy of IntegrationInterpreting Accuracy 6Integrating Equations 8        8Integrating Equations 8 Form  Operations with Complex Numbers 2Operations with Complex Numbers Complex StackComplex Operations Functions for One Complex Number, z To Calculate Press 8  6 6 6 8  6Display Description 4Operations with Complex Numbers Using Complex Numbers in Polar Notation 6Operations with Complex Numbers ?  ?  ?  6 ? ? Complex Numbers in Equations Complex Number in Program Program lines ALG mode          Vector Arithmetic Vector ArithmeticVector operations    Õ 3   3  Absolute value of the vector    Dot product3 3 10-4Vector Arithmetic  Õ Angle between vectors  3   10-6Vector Arithmetic Vectors in Equations3   Program lines Description Vectors in Programs 10-8Vector Arithmetic Creating Vectors from Variables or RegistersThen hC Õ hA Base Menu Base Conversions and Arithmetic and LogicMenu label Description Base Conversions and Arithmetic and Logic 11-2Base Conversions and Arithmetic and Logic    Õ  11-4Base Conversions and Arithmetic and Logic Arithmetic in Bases 2, 8,Logic Menu          Negative Numbers Representation of Numbers   Range of Numbers Windows for Long Binary Numbers Using base in program and equations    Statistical Operations Statistical OperationsEntering Statistical Data Entering One-Variable Data Correcting Errors in Data EntryEntering Two-Variable Data 12-2Statistical Operations Initial x, y Corrected x, y   Mean Statistical CalculationsStatistics Menus Menu Key Description   Sample Standard Deviation        Linear Regression Population Standard Deviation 12-8Statistical Operations  ˆ Õ ˆLinear Regression Menu        12-10Statistical Operations Limitations on Precision of Data Summation Statistics Summation Values and the Statistics Registers 12-12Statistical Operations Access to the Statistics Registers Statistical Operations 12-14Statistical Operations Programming Page Simple Programming Simple Programming Area = πx2 13-2Simple Programming KeysDisplay In ALG mode Selecting a ModeDesigning a Program  X  Program Boundaries LBL and RTN Using RPN, ALG and Equations in Programs13-4Simple Programming  letter-key Strengths of RPN Operations Data Input and Output 13-6Simple Programming Entering a Program Clear functions and backspace key 13-8Simple Programming Function Names in ProgramsA E RPN modeR  R  Executing a Program XEQ Running a Program 13-10Simple Programming  Testing a ProgramKeys Display Description RPN mode 13-12Simple Programming Entering and Displaying Data RPN mode ALG mode Using Input for Entering Data 13-14Simple Programming Using View for Displaying Data 13-16Simple Programming Using Equations to Display Messages  ÇR ÇH  R H V  R R H  Keys RPN mode V OL  A RE A    V  S       Displaying Information without Stopping13-18Simple Programming C  value Stopping or Interrupting a Program Error StopsProgramming a Stop or Pause STOP, PSE Interrupting a Running Program 13-20Simple Programming Editing a Program Viewing Program Memory Program Memory 13-22Simple Programming Memory UsageCatalog of Programs MEM Checksum Clearing One or More Programs Programming with Base Nonprogrammable Functions   Numbers Entered in Program Lines Selecting a Base Mode in a ProgramDecimal mode set Ax4 + Bx3 + Cx2 + Dx + E Polynomial Expressions and Horners Method13-26Simple Programming A    A X     13-28Simple Programming Routines in Programs Programming TechniquesCalling Subroutines XEQ, RTN Programming Techniques 14-2Programming Techniques Nested Subroutines A2 + b2 + c2 + d2 A2 + B2 Branching GTO14-4Programming Techniques Programmed GTO Instruction Using GTO from the Keyboard 14-6Programming Techniques Conditional Instructions Test Menus Tests of Comparison x?y, x?0 14-8Programming Techniques Program Lines Description RPN mode Meanings of Flags Flags 14-10Programming Techniques Flag Fraction-Control FlagsClear Programming Techniques 14-12Programming Techniques Flags Menu … takes the natural log of the X-input S  value   value  14-14Programming Techniques Number 14-16Programming Techniques LoopsF      Conditional Loops GTO 14-18Programming Techniques Loops with Counters DSE, ISG Programming Techniques 14-20Programming Techniques Indirectly Addressing Variables and LabelsVariables I and J Indirect Address, I and J 14-22Programming Techniques If I/J contains Then I/J will address Unnamed indirect variables Program Control with I/JEquations with I/J 14-24Programming Techniques Solving and Integrating Programs Solving and Integrating ProgramsSolving a Program V= N x R x T 15-2Solving and Integrating Programs Program Lines Description ALG mode Keys Display Description ALG modeG P  value   value   H     LP   label  variable Using Solve in a Program15-6Solving and Integrating Programs Integrating a Program Program Lines In RPN mode 15-8Solving and Integrating Programs Sin  S   X  label   variable Using Integration in a Program15-10Solving and Integrating Programs Restrictions on Solving and Integrating 15-12Solving and Integrating Programs Statistics Programs Statistics ProgramsCurve Fitting 16-2Statistics Programs = B + MIn Program Listing 16-4Statistics Programs    16-6Statistics Programs Determines if D001 or B001 should be run 16-8Statistics Programs   S          Normal and Inverse-Normal Distributions Logarithmic Exponential Power  16-12Statistics Programs Qx = 0.5 − σ 12π xx e−x −x ⎟σ 2 ⎟2dx This routine initializes the normal distribution program 16-14Statistics Programs Program Lines Program Lines 16-16Statistics Programs S To the inverse Program D  ∑ x f Grouped Standard Deviation16-18Statistics Programs   16-20Statistics Programs Register Summation Σ f Summation Σ x i f Index variable used to indirectly address the correctStatistics register    U     16-24Statistics Programs Time Value of Money Miscellaneous Programs and EquationsMiscellaneous Programs and Equations TVM equation is 4 PI NÕ I     KeysDisplay In RPN mode17-4Miscellaneous Programs and Equations P  value     I 17-6Miscellaneous Programs and Equations   Prime Number Generator 17-8Miscellaneous Programs and Equations Tests to see whether all possible factors have been tried 17-10Miscellaneous Programs and Equations   Cross Product in Vectors 17-12Miscellaneous Programs and Equations z 17-14Miscellaneous Programs and Equations Appendixes and Reference Page Support, Batteries, and Service A-1 Support, Batteries, and ServiceCalculator Support Answers to Common Questions Environmental Limits 2Support, Batteries, and Service Changing the Batteries Support, Batteries, and Service A-3 4Support, Batteries, and Service Testing Calculator Operation Self-Test Support, Batteries, and Service A-5 6Support, Batteries, and Service Support, Batteries, and Service A-7 Warranty Customer Support 8Support, Batteries, and Service Emea Support, Batteries, and Service A-9 10Support, Batteries, and Service Invent Support, Batteries, and Service A-11 12Support, Batteries, and Service Yyyy+ Support, Batteries, and Service A-13 14Support, Batteries, and Service User Memory and the Stack B-1 User Memory and the StackManaging Calculator Memory 2User Memory and the Stack Resetting the Calculator User Memory and the Stack B-3 Clearing Memory Status of Stack Lift DefaultCategory 4User Memory and the Stack User Memory and the Stack B-5 Disabling OperationsNeutral Operations 6User Memory and the Stack Status of the Last X Registerˆ ˆ Accessing Stack Register Contents 8User Memory and the Stack About ALG ALG Summary, ALG Summary C-1 Simple Arithmetic Doing Two argument Arithmetic in ALG Percentage Calculations Power Functions Permutations and Combinations Parentheses CalculationsQuotient and Remainder Of Division xÕ Õ 4   Hyperbolic functions Trigonometric Functions ALG Summary C-7 Reviewing the Stack 8ALG Summary Integrating an EquationOperations with Complex Numbers ALG Summary C-9 6 4 66 8Ë 6Õ4 6 Entering Statistical Two-Variable Data 12ALG Summary z ΣZ6 ALG Summary C-13   ˆ Õ ˆ 14ALG Summary More about Solving D-1 More about SolvingHow Solve Finds a Root Function Whose Roots Can Be Found 2More about Solving More about Solving D-3 Interpreting Results X  X X  X 4More about Solving X XX   6More about Solving XÕ  X4 X  X Õ  More about Solving D-7 8More about Solving When Solve Cannot Find a Root X   More about Solving D-9  X   X   X  10More about Solving More about Solving D-11 X4 X ÕÕ 12More about Solving X   More about Solving D-13 Round-Off Error X   14More about Solving More about Integration More about IntegrationHow the Integral Is Evaluated 2More about Integration Conditions That Could Cause Incorrect Results ∞ xe−xdx 4More about Integration   More about Integration 6More about Integration   Conditions That Prolong Calculation Time 8More about Integration More about Integration 10More about Integration Messages F-1 Messages Or program. This might take a while 2Messages Messages F-3    Solve include EQN and PGM modecannot find 4Messages Messages F-5 FN each uses a level, they can also generate this error 6Messages Operation Index G-1 Operation IndexName Keys and Description 2Operation Index ×Ø Operation Index G-3 4Operation Index =  Denominator Operation Index G-5 6Operation Index Natural exponential Operation Index G-7label  Fractional part 8Operation Index  Operation Index G-9 Input variable variable  Integer part ISG variable variable 10Operation Index LBL label label Natural logarithm RCL variable Operation Index G-11 Pause Degrees to radians. Returns 2π/360 12Operation Index Operation Index G-13 Hyperbolic Tangent 14Operation IndexView variable variable XEQ label label ≠ ÕÕÕ≤ Operation Index G-15 =y? 16Operation Index14-7 Menu ≠0? 11-4 Operation Index G-17 Power 18Operation Index Index-1 Index Index-2 EQN List TOP 6-7, F-2 Index-3 Index-4 Index-5 Index-6 Index-7 Index-8 Index-9 Index-10 Angle between two vectors Index-11 Index-12