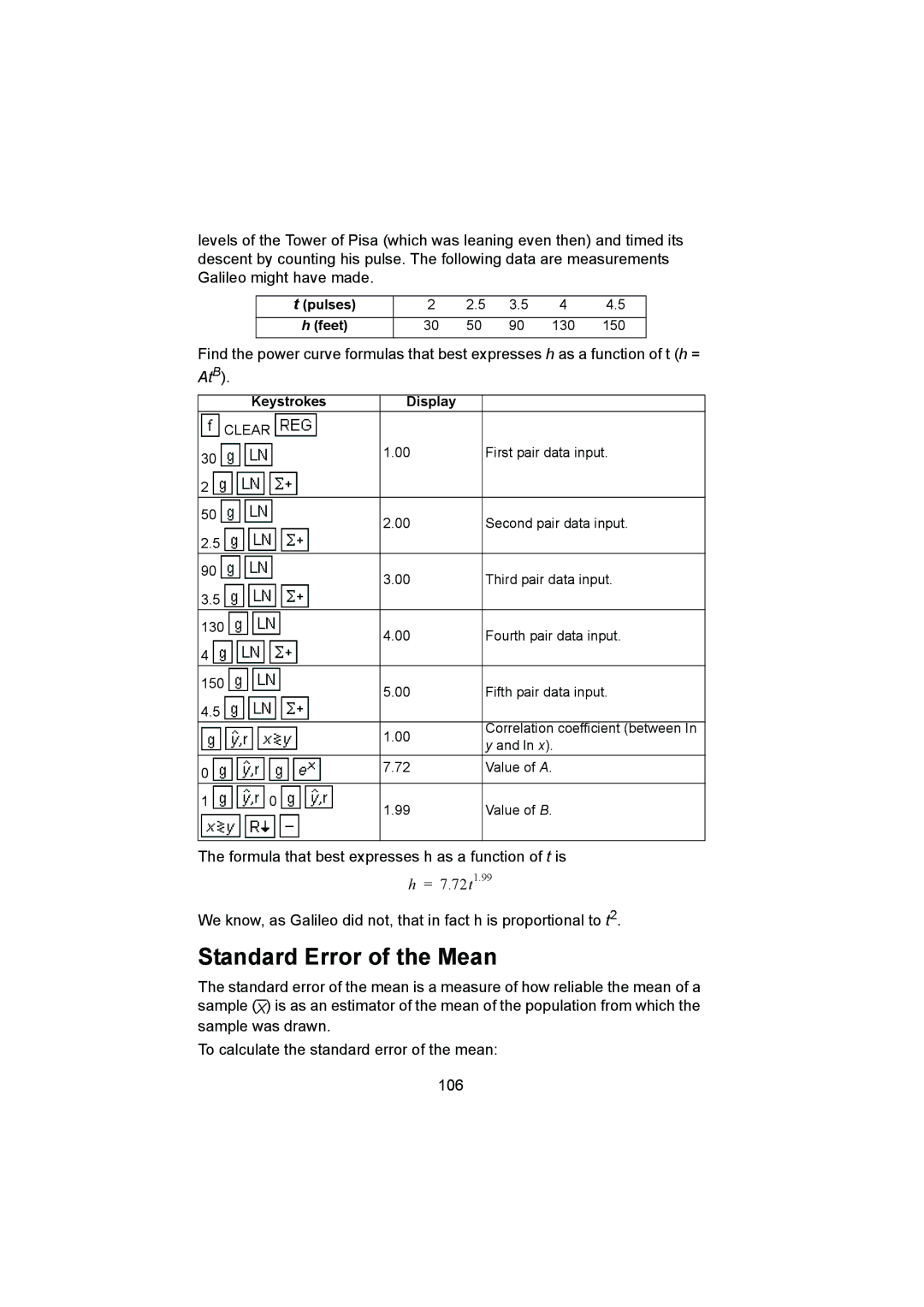
levels of the Tower of Pisa (which was leaning even then) and timed its descent by counting his pulse. The following data are measurements Galileo might have made.
t (pulses) | 2 | 2.5 | 3.5 | 4 | 4.5 |
h (feet) | 30 | 50 | 90 | 130 | 150 |
Find the power curve formulas that best expresses h as a function of t (h =
AtB).
| Keystrokes | Display |
|
| CLEAR |
|
|
30 |
| 1.00 | First pair data input. |
|
|
| |
2 |
|
|
|
50 |
| 2.00 | Second pair data input. |
|
| ||
2.5 |
|
|
|
90 |
| 3.00 | Third pair data input. |
|
| ||
3.5 |
|
|
|
130 |
| 4.00 | Fourth pair data input. |
|
| ||
4 |
|
|
|
150 |
| 5.00 | Fifth pair data input. |
|
| ||
4.5 |
|
|
|
|
| 1.00 | Correlation coefficient (between In |
|
| y and ln x). | |
|
|
| |
0 |
| 7.72 | Value of A. |
|
|
| |
1 | 0 | 1.99 | Value of B. |
|
| ||
|
|
|
|
The formula that best expresses h as a function of t is
h= 7.72t1.99
We know, as Galileo did not, that in fact h is proportional to t2.
Standard Error of the Mean
The standard error of the mean is a measure of how reliable the mean of a sample (X) is as an estimator of the mean of the population from which the sample was drawn.
To calculate the standard error of the mean:
106