Allied Telesis AT-9724TS specifications Shortest Path Tree, 104

Shortest Path Tree

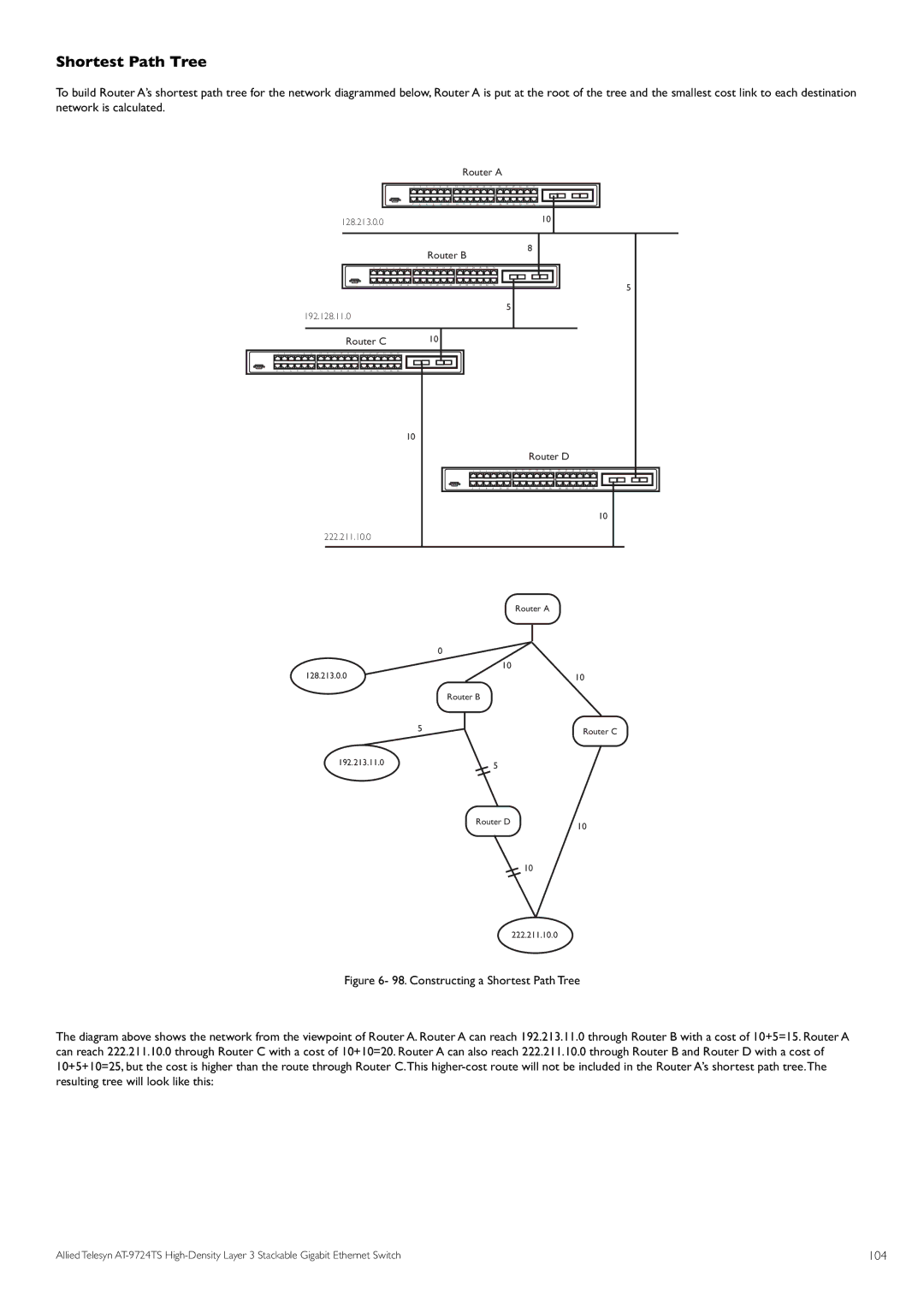
To build Router A’s shortest path tree for the network diagrammed below, Router A is put at the root of the tree and the smallest cost link to each destination network is calculated.

Router A

1	3	5	7	9	11	13	15	17	19	21	23	25	27	29	31	33	35
2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36
128.213.0.0																	10

Router B

8

1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35

2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36

5

192.128.11.0

Router C 10

5

1	3	5	7	9	11	13	15	17	19	21	23	25	27	29	31	33	35
2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36

10

Router D

1	3	5	7	9	11	13	15	17	19	21	23	25	27	29	31	33	35
2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36

10

222.211.10.0

			Router A
		0
128.213.0.0		10
			10
		Router B
	5		Router C
192.213.11.0		5
		Router D	10

10

222.211.10.0

Figure 6- 98. Constructing a Shortest Path Tree

The diagram above shows the network from the viewpoint of Router A. Router A can reach 192.213.11.0 through Router B with a cost of 10+5=15. Router A can reach 222.211.10.0 through Router C with a cost of 10+10=20. Router A can also reach 222.211.10.0 through Router B and Router D with a cost of 10+5+10=25, but the cost is higher than the route through Router C.This higher-cost route will not be included in the Router A’s shortest path tree.The resulting tree will look like this:

Allied Telesyn AT-9724TS High-Density Layer 3 Stackable Gigabit Ethernet Switch 104