Intel 80287, 80286 manual Denormalization Process, Overview of Numeric Processing

OVERVIEW OF NUMERIC PROCESSING

were long real or temporary real, since these formats can handle exponents down to -1023 and -16,383, respectively.

Most computers underflow "abruptly:" they simply return a zero result, which is likely to produce an unacceptable final result if computatiol). continues. The 80287, on the other hand, underflows "gradu- ally" when the underflow exception is masked. Gradual underflow is accomplished by denormalizing the result until it is just within the exponent range of the destination format.- Denormalizing means incrementing the true result's exponent and inserting a corresponding leading zero in the significand, shifting the rest of the significand one place to the right. Denormal values may occur in any of the short-real, long-real, or temporary-real formats. Table 1-7 illustrates how a result might be denormal- ized to fit a short-real destination.

The intent of the 80287's masked response to underflow is to allow computation to continue without program intervention, while introducing an error that carries about the same risk of contaminating the final result as roundoff error. Roundoff (precision) errors occur frequently in real number calculations; sometimes they spoil the result of computation, but often they do not. Recognizing that roundoff errors are often nonfatal, computation usually proceeds, and the programmer inspects the final results to see if these errors have had a significant effect. The 80287's masked underflow response allows program- mers to treat underflows in a similar manner; the computation continues and the programmer can examine the final result to determine if an underflow has had important. consequences. (If the underflow has had a significant effect, an invalid operation will probably be signalled later in the computation.)

Denormalization produces a denormal or a zero. Denormals are readily identified by their exponents, which are always the minimum for their formats; in biased form, this is always the bit string: 00...00. This same exponent value is also assigned to the zeros, but a denormal has a nonzero significand. A denormal in a register is tagged special. Tables 1-14 and 1-15 later in this chapter.show how denormal values are encoded in each of the real data formats.

The denormalization process may cause the loss of low-order significand bits as they are shifted off the right. In a severe case, all the significand bits of the true result are shifted out and replaced by the leading zeros. In this case, the result of denormalization is a true zero, and if the value is in a register, it is tagged as such. However, this is a comparatively rare occurrence and, in any case, is no worse than "abrupt" underflow.

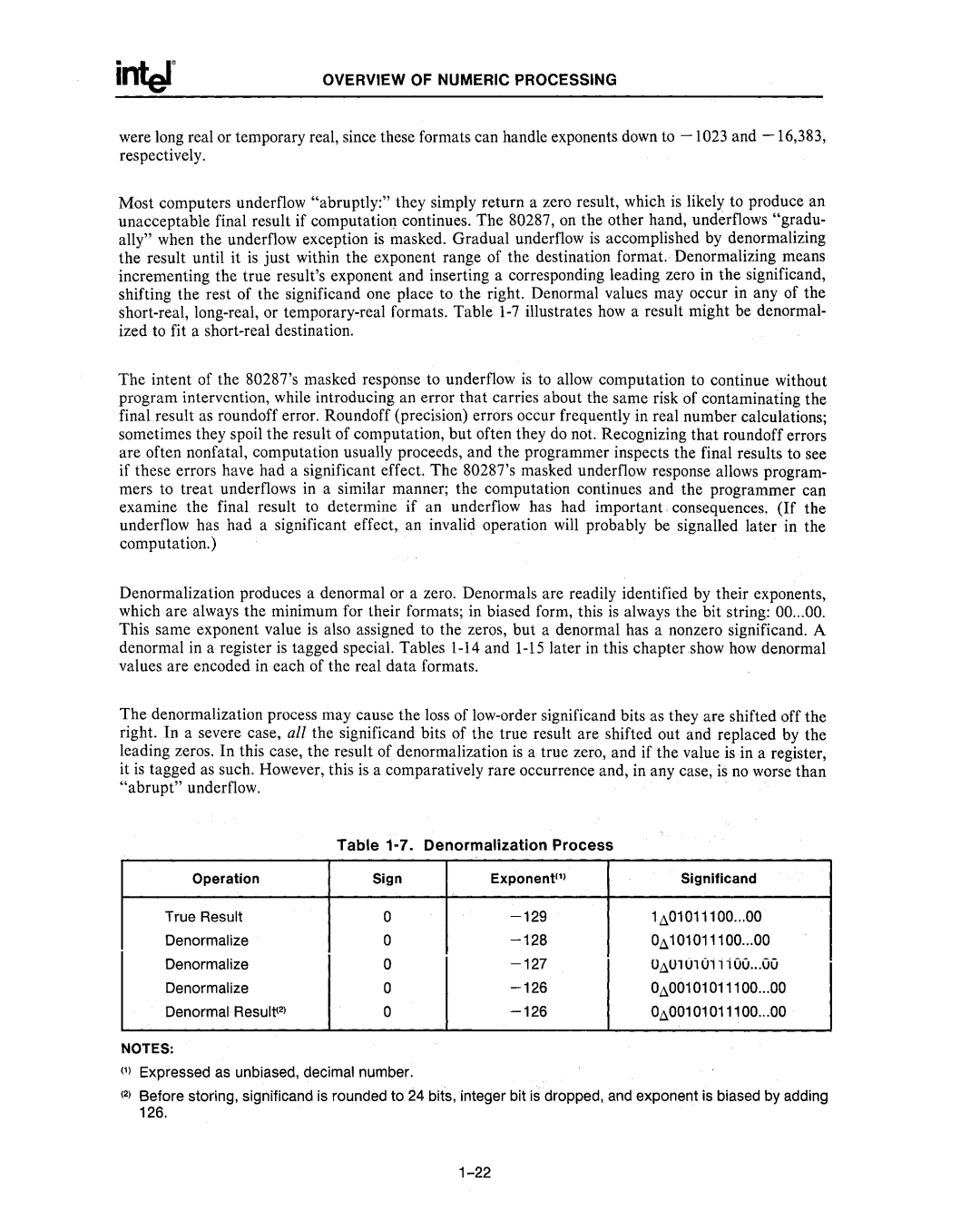
Table 1-7. Denormalization Process

Operation	Sign	Exponent(')	Significand
True Result	0	-129	1.l01 0111 00...00
Denormalize	0	-128	0.l1 01	0111 00...00
Denormalize	0	-127	U.lU1 01 0;;; 00 ...00
Denormalize	0	-126	0.l001	01 0111 00 ... 00
Denormal Result(2)	0	-126	0.l001	01 0111 00 ... 00

NOTES:

(') Expressed as unbiased, decimal number.

(2)Before storing, significand is rounded to 24 bits, integer bit is dropped, and exponent is biased by adding

126.

1-22