DSP56000
OnCE is a trade mark of Motorola, Inc Motorola Inc
DSP56K Family
Semiconductor
OnCETM is a trade mark of Motorola, Inc
Table of Contents
Table of Contents Motorola
Number Title
Methods of Entering the Debug Mode
Port a Overview Port a Interface
ON-CHIP Emulation Introduction
Pipeline Information and Global Data BUS Register
Appendix a Instruction SET Details
Motorola
List of Figures Vii Revision
List of Figures Number Title
Viii
List of Figures Number Title
List of Tables
List of Tables Number Title
Xii
Section DSP56K Family Introduction
Motorola DSP56K Family Introduction
Section Contents
Origin of Digital Signal Processing
Introduction
Analog Signal Processing
Digital Signal Processing
Benchmark Summary in Instruction Cycles
Benchmark Number of Cycles Algorithm Multiplies
Signal Processing
Digital Filtering
Data Processing
Numeric Processing
Audio Signal Processing
Image Processing
Graphics
Instrumentation
Summary of DSP56K Family Features
DSP Hardware Origins
Summary of DSP56K Family Features
Manual Organization
Manual Organization
Section DSP56K Central Architecture Overview
Motorola DSP56K Central Architecture Overview
PHASE-LOCKED Loop PLL Based Clocking
DSP56K Central Architecture Overview Motorola
Data Buses
DSP56K Block Diagram
Address Buses
Internal Bus Switch
Data ALU
Bit Manipulation Unit
Address Generation Unit
Memory Expansion Port Port a
PHASE-LOCKED Loop PLL Based Clocking
ON-CHIP Emulator OnCE
Section Data Arithmetic Logic Unit
Motorola Data Arithmetic Logic Unit
Data Arithmetic Logic Unit Motorola
Overview and Data ALU Architecture
DSP56K Block Diagram
Data ALU Input Registers X1, X0, Y1, Y0
Data ALU
MAC and Logic Unit
MAC Unit Data ALU a and B Accumulators
Data ALU Accumulator Registers
Data Shifter/Limiter
Accumulator Shifter
Limiting Saturation Arithmetic
Data Representation and Rounding
Scaling
Limited Data Values
Integer-to-Fractional Data Conversion
Bit Weighting and Alignment of Operands
Integer/Fractional Number Comparison
Integer/Fractional Multiplication Comparison
10 Convergent Rounding
Double Precision Multiply Mode
MSP1 LSP1 DP3 DP1 MSP2 LSP2 DP2 DP0
MSP1 LSP1 DP3 DP1 DP2
12 Single ⋅ Double Multiply Algorithm
DP3 DP1
13 Single ⋅ Double Multiply-Accumulate Algorithm
Data ALU Programming Model
Data ALU Summary
Data ALU Summary Data Arithmetic Logic Unit Motorola
Section Address Generation Unit
Motorola Address Generation Unit
Addressing
Programming Model
Address Generation Unit Motorola
AGU Architecture
Address Generation Unit and Addressing Modes
Address Register Files Rn
DSP56K Block Diagram Offset Register Files Nn
Modifier Register Files Mn
Address ALU
Programming Model
Address Output Multiplexers
AGU Programming Model Address Register Files R0 R3 and R4 R7
Offset Register Files N0 N3 and N4 N7
Address Register Indirect Summary
Addressing
Modifier Register Files M0 M3 and M4 M7
No Update
Address Register Indirect Modes
Postincrement By
Postdecrement By
Address Register Indirect No Update
Postincrement By Offset Nn
Address Register Indirect Postincrement
Postdecrement By Offset Nn
Address Register Indirect Postdecrement
Indexed By Offset Nn
Address Register Indirect Postincrement by Offset Nn
Predecrement By
Address Register Indirect Postdecrement by Offset Nn
Address Modifier Arithmetic Types
Address Register Indirect Indexed by Offset Nn
10 Address Register Indirect Predecrement
Linear Modifier Mn=$FFFF
Modulo Modifier
2.2.1 Mn=$0001 to $7FFF
Address Modifier Summary
Mmmm
11 Circular Buffer
12 Linear Addressing with a Modulo Modifier
13 Modulo Modifier Example
2.2.2 Mn=$8001 to $BFFF
Reverse-Carry Modifier Mn=$0000
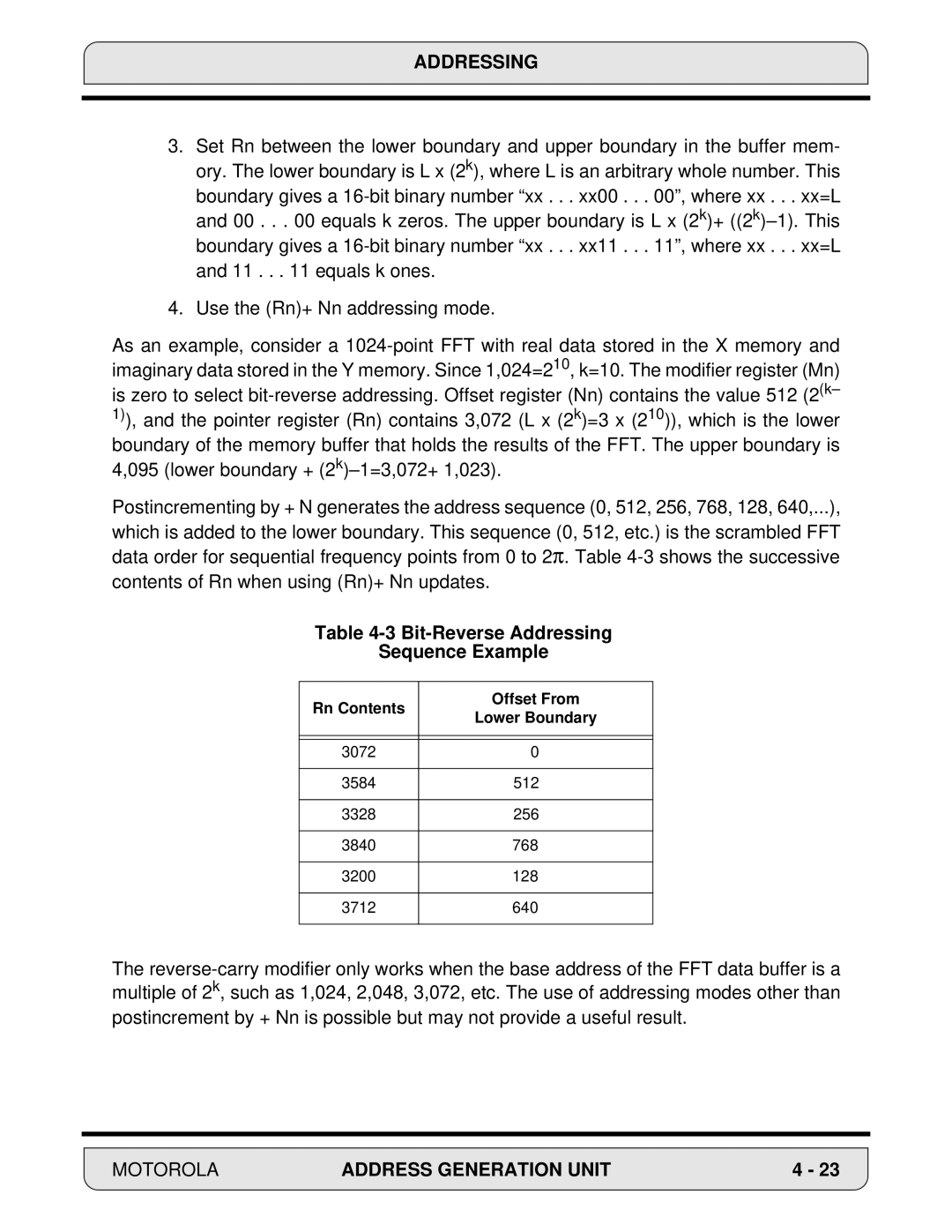
Bit-Reverse Addressing Sequence Example
14 Bit-Reverse Address Calculation Example
Addressing
15 Address Modifier Summary
Section Program Control Unit
Motorola Program Control Unit
Program Control Unit Motorola
Overview
Program Address Generator
24-Bit
Program Decode Controller
Program Control Unit PCU Architecture
Program Address Generator PAG
Tion 7 Processing States
Program Interrupt Controller
Instruction Pipeline Format
Three-Stage Pipeline
Program Control Unit Programming Model
Program Counter
Status Register Format
Status Register
Carry Bit
Overflow Bit
Zero Bit
Negative Bit
Limit Bit
Extension Bit
Scaling Bit Bit
Scaling Mode Bits 10
Interrupt Masks Bits 8
Double Precision Multiply Mode Bit
Trace Mode Bit
Reserved Status Bit
Loop Flag Bit
Operating Mode Register
System Stack
Stack Pointer Register Format
Stack Pointer Bits
Stack Error Flag Bit
SP Register Values
Underflow Flag Bit
Reserved Stack Pointer Registration Bits
Loop Address Register
Loop Counter Register
DSP56K Central Processing Module Programming Model
Section Instruction SET Introduction
Motorola Instruction SET Introduction
Instruction Groups
Instruction SET Introduction Syntax Instruction Formats
Instruction SET Introduction Motorola
Syntax
Opcode Operands
XDB YDB
MAC
Operating Mode Register OMR
Appendix a Instruction SET Details
Operand Sizes
Operand Sizes Data Organization in Registers
Data ALU Registers
Reading and Writing the ALU Extension Registers
16 Bit
Bit
Data Organization in Memory
Addresses
Program Control Unit
Miscellaneous
Operand References
Program References
Stack References
Register References
Instruction Formats
YX Memory References
Addressing Modes
Data or Control Register Direct
Register Direct Modes
Address Register Direct
Special Addressing Modes
Immediate Data
Absolute Address
Immediate Short
Special Addressing Immediate Data
Implicit Reference
5.3.6 I/O Short
Addressing Modes Summary
Before Execution After Execution X X X
Instruction Groups
Arithmetic Instructions
11 Special Addressing Absolute Short Address
12 Special Addressing I/O Short Address
Modifier Operand Reference Addressing Mode
Logical Instructions
Andi
EOR
LSL
LSR
Bit Manipulation Instructions
Loop Instructions
13 Hardware do Loop
LUA
Move
Movec
Movem
Debug
Program Control Instructions
JMP
Reset
Jclr
Jset
JSR
Instruction Groups Instruction SET Introduction Motorola
Section Processing States
Motorola Processing States
Exception Processing State
Processing States Normal Processing State
Processing States Motorola
Instruction Pipeline
Normal Processing State
Instruction Pipelining
ORI #04,OMR
Bootend Movec
Inst
Inst Inst 3 Inst
Andi #00,MR
Do instruction restrictions
Summary of Pipeline-Related Restrictions
Restrictions near the end of do loops
Enddo instruction restrictions
RTI and RTS instruction restrictions
Exception Processing State Interrupt Processing
SP and SSH/SSL register manipulation restrictions
BCHG/BCLR/BSET SP
Rn, Nn, and Mn register restrictions
Interrupt Types
Interrupt Priority Structure
DSP56K Fast Interrupt
DSP56K Long Interrupt
Interrupt Priority Levels
Status Register Interrupt Mask Bits
Exception Priorities Within an IPL
Interrupt Sources
Interrupt Priority Level Bits External Interrupt
Central Processor Interrupt Priorities Within an IPL
Hardware Interrupt Sources
Starting Address
Interrupting an SWI
Software Interrupt Sources
Instruction Fetches from Memory
Program Controller Pipeline
Illegal Instruction Interrupt Serviced by a Long Interrupt
Repeated Illegal Instruction
Other Interrupt Sources
Main Program Fetches
Interrupt Arbitration
Interrupt Instruction Fetch
Instructions Preceding the Interrupt Instruction Fetch
Interrupt Instruction Execution
Fast Interrupt Service Routine
Two Consecutive Fast Interrupts
Exception Processing State Interrupt Processing
10 Long Interrupt Service Routine
11 JSR First Instruction of a Fast Interrupt
12 JSR Second Instruction of a Fast Interrupt
Reset Processing State
13 Interrupting an REP Instruction
14 Interrupting Sequential REP Instructions
Wait Processing State
15 Wait Instruction Timing
Stop Processing State
16 Simultaneous Wait Instruction and Interrupt
17 Stop Instruction Sequence
18 Stop Instruction Sequence Followed by Irqa
Stop Processing State
Stop Processing State
19 Stop Instruction Sequence Recovering with Reset
Stop Processing State Motorola Processing States
Stop Processing State Processing States Motorola
Section Port a
Motorola Port a
Port a Motorola
Port a Overview
Port a Interface
Port a Signals
Read/Write Control Signals
Port a Address and Data Bus Signals
Program Memory Select PS
Data Memory Select DS
Port a Bus Control Signals
Read Enable RD
Write Enable WR
Address A0-A15
Port a Interface
Port a Interface Motorola
Section PLL Clock Oscillator
Motorola PLL Clock Oscillator
PLL Clock Oscillator Introduction PLL Components
PLL Pins PLL Operation Considerations
PLL Clock Oscillator Motorola
PLL Components
PLL Clock Oscillator Introduction
VCO
Area
Low Power Divider LPD
Voltage Controlled Oscillator VCO
Frequency Multiplier
PLL Control Register Pctl
Pctl Division Factor Bits DF0-DF3 Bits
Division Factor Bits DF0-DF3
Pctl Xtal Disable Bit Xtld Bit
Pctl Stop Processing State Bit Pstp Bit
Pctl Clock Output Disable Bits COD0-COD1 Bits
Pctl PLL Enable Bit PEN Bit
Pstp and PEN Relationship
PLL Pins
Clock Output Disable Bits COD0-COD1
Pctl Chip Clock Source Bit Csrc Bit
Pctl Ckout Clock Source Bit Ckos Bit
PLL Pins
PLL Operation Considerations
Hardware Reset
Operating Frequency
Changing the MF0-MF11 Bits
Operation with PLL Disabled
Change of DF0-DF3 Bits
Stop Processing State
Loss of Lock
Ckout Considerations
Synchronization Among EXTAL, CKOUT, and the Internal Clock
Section
ON-CHIP Emulation OnCE
Introduction
ON-CHIP Emulation Introduction
Debug Serial Input/Chip Status 0 DSI/OS0
24X24+56 →56-BIT MAC OnCE
Chip Status Information
OS1 OS0
Status
Debug Serial Output DSO
OnCE Controller and Serial Interface Debug Request Input DR
OnCE Command Register OCR
OnCE Controller and Serial Interface
RS4 RS3 RS2 RS1 RS0
OnCE Register Addressing
OnCE Controller and Serial Interface Exit Command EX Bit
Go Command GO Bit
Read/Write Command R/W Bit
Action
OnCE Decoder Odec
OnCE Status and Control Register Oscr
Memory Breakpoint Control BC0-BC3 Bits
MBO SWO TME BC3
Memory Breakpoint Control Table
Trace Mode Enable TME Bit
Reserved Bits 5-7
Memory Breakpoint Occurrence MBO Bit
Trace Occurrence to Bit
OnCE Memory Breakpoint Logic
Memory Address Latch Omal
Isbkpt
Memory Lower Limit Register Omllr
OnCE Trace Logic
Memory High Address Comparator Omhc
Memory Low Address Comparator Omlc
Memory Breakpoint Counter Ombc
OnCE Trace Logic Block Diagram Trace Counter OTC
Istrace
Methods of Entering the Debug Mode
External Debug Request During Reset
External Debug Request During Normal Activity
External Debug Request During Stop
Enabling Trace Mode
Pipeline Information and Global Data BUS Register
Software Request During Normal Activity
Enabling Memory Breakpoints
Program Address BUS History Buffer
Pipeline Instruction Latch Register Opilr
Global Data Bus Register Ogdbr
Read GDB Register
PAB Register for Fetch Opabfr
PAB Register for Decode Opabdr
Serial Protocol Description
OnCE Commands
PAB Fifo
Using the OnCE
Begin Debug Activity
Displaying a Specified Register
Motorola
Motorola
Motorola
Returning from Debug Mode to Normal Mode
Motorola
Motorola
Motorola
Section Additional Support
Motorola Additional Support
User Support Motorola DSP Product Support
Motorola DSP News Motorola Field Application Engineers
13 Reference Books and Manuals
Additional Support Motorola
User Support
Motorola Third Party Design
Prototyping
Verification
Macro Cross Assembler Features
Motorola DSP Product Support
Simulator Features
11.2.4 DSP56KCCx Language Compiler Features
DSP56KADSx Application Development System
11.4 Dr. BuB Electronic Bulletin Board
Dr. BuB Electronic Bulletin Board
Audio
Codec Routines
Dtmf Routines
Document ID Version Synopsis Size
Fast Fourier Transforms
Filters
Floating-Point Routines
Functions
Lattice Filters
Matrix Operations
=AB+Q
Reed-Solomon Encoder
Sorting Routines
Speech
Standard I/O Equates
Tools and Utilities
Following is a list of current DSP56200 related software
Motorola Field Application Engineers
Motorola DSP News
THIRD-PARTY Support Information 512
Reference Books and Manuals
Training Courses 602 897-3665 or 800
General DSP
Digital Audio and Filters
Adaptive Signal Processing
Digital Audio Signal Processing AN Anthology
Digital Filters and Signal Processing
ART of Digital AUDIO,
Programming Language
Controls
CGM and CGI
Fundamentals of Interactive Computer Graphics
Geometric Modeling
GKS Theory and Practice
Motorola DSP Manuals
Numerical Methods
Pattern Recognition
Telecommunications
Motorolaola Routines
Section Contents
Third Party Support
Motorola DSP Product Support
Application Development Systems
Support Integrated Circuits
DSP Applications Help Line 512
DSP Marketing Information 512
DSP THIRD-PARTY Support Information 512
DSP University Support 512
DSP Training Courses 602 897-3665 or 800
12.13 Dr. BuB Electronic Bulletin Board
Benchmarks
Document ID Version Synopsis Size
Filters
Floating-Point Routines
Functions
Lattice Filters
Document ID Version
Current DSP56200 Related Software
Reference Books and Manuals
Digital Audio and Filters
Leland B. Jackson Higham, MA Kluwer Academic Publishers
Illumination and Color in Computer Generated Imagery
Motorola DSP LINKER/LIBRARIAN Reference Manual
Motorola DSP Assembler Reference Manual
Motorola DSP Simulator Reference Manual
Motorola DSP56100 Family Manual
Motorola DSP56156 USER’S Manual
Statistical Spectral ANALYSIS, a Nonprobabilistic Theory
Digital Communications
Appendix a Instruction SET Details
Motorola Instruction SET Details
Section A.10 Instruction Encoding
Section A.9 Instruction Sequence Restrictions
Instruction SET Details Motorola
Appendix a Introduction
Instruction Guide
Notation
Address ALU Registers Operands
Address Operands
OMR
Unary Operators
Binary Operators
Mode Register MR Symbols
Condition Code Register CCR Symbols
Other Symbols
MSP
Addressing Modes
Table A-2 DSP56K Addressing Modes
D a P X Y L XY
Table A-3 DSP56K Addressing Mode Encoding
M a
Addressing Mode Modifiers
Table A-4 Addressing Mode Modifier Summary
Binary M0-M7 Hex M0-M7 Addressing Mode Arithmetic
Condition Code Computation
Condition Code Computation
Scaling Mode Signed Integer Portion
Scaling Mode Bit Computation
Condition Code Computation
Following notes apply to Table A-5
Parallel Move Descriptions
Instruction Descriptions
Operation Assembler Syntax
Absolute Value
Condition Codes
Instruction Format
ABS D
Opcode
Instruction Fields
Add Long with Carry
Example
ADC S,D
Add
ADD S,D
Instruction Fields J d
Shift Left and Add Accumulators
Addl S,D
Shift Right and Add Accumulators
Addr S,D
Logical Operation Assembler Syntax
Logical
S,D
Immediate with Control Register
CCR OMR
Arithmetic Shift Accumulator Left
ASL D
Arithmetic Shift Accumulator Right
ASR D
Bit Test and Change
CCR Condition Codes
Not affected Set if bit tested is set. Cleared otherwise
For other destination operands
M R R R
Effective Addressing Mode
Memory SpaceS Bit Number bbbbb
Absolute Short Address aaaaaa Memory SpaceS Bit Number bbbbb
Short Address pppppp Memory SpaceS Bit Number bbbbb
Destination Register
D D D D
Bchg
Bit Test and Clear
Condition Codes
For other destination operands
Bclr #n,Xea Bclr #n,Yea
Bclr #n,Xaa Bclr #n,Yaa
Bclr #n,Xpp Bclr #n,Ypp
Bclr #n,D
Bclr
Bset
Bit Test and Set Operation Assembler Syntax
Bit Test and Set
For other destination operands
Bset #n,Xea Bset #n,Yea
0 0 1 0 1 A a 1 b b b b b
0 0 1 0 1 P p 1 b b b b b
Bit Test and Set Instruction Format
Bset
Bit Test
For destination operand a or B
Btst #n,Xea Btst #n,Yea
Btst #n,Xaa Btst #n,Yaa
Btst #n,Xpp Btst #n,Ypp
Btst #n,D
Clear Accumulator
Always cleared Always set
CLR D
Compare
Instruction Fields S1,S2 J d
Compare Magnitude
Cmpm S1, S2
Debug
Timing 4 oscillator clock cycles Memory 1 program word
CC HS
Cc Mnemonic Condition
CS LO
Enter Debug Mode Conditionally DEBUGcc
CMP Y0, B
Instruction Fields Mnemonic
CC HS CS LO
Decrement by One
DEC D
Instruction Fields
DIV S,D
Divide Interation
Description
DIV
ABS a A,B
#$FE,CCR
DIV X0,A
TFR A,B
Signed quotient and a 48-bit signed remainder
ADD X0,A
Set if overflow bit V is set
0 0 0 0 0 J d 0 0
Start Hardware Loop Operation Assembler Syntax
Start Hardware Loop
At LA-2, LA-1, and LA
Andi MR
ORI MR
At LA-1
Jclr Reset Jset RTI JMP RTS
Start Hardware Loop At LA
JSR Wait
Other Restrictions
END2
END1
Xea, expr
Absolute Short Address aaaaaa Memory SpaceS
Immediate Short Data hhhh i i i i i i i
Source
OMR SSL
Start Hardware Loop
End Current do Loop
Immediately before Enddo
Opcode Instruction Fields
Logical Exclusive or
EOR S,D
Illegal Instruction Interrupt
Illegal
None Timing 8 oscillator clock cycles Memory 1 program word
Increment by One
INC D
Jcc
Jump Conditionally
0 0 1 1 1 C C a a a a A a a a a a
Jcc ea
M R R R
Jump if Bit Clear
For other source operands Condition codes are not affected
Jclr #n,Xea,xxxx Jclr #n,Yea,xxxx
Jclr #n,Xaa,xxxx Jclr #n,Yaa,xxxx
Jclr #n,Xpp,xxxx Jclr #n,Ypp,xxxx
Source Register
Jump
0 0 1 0 1 M M R R R 0 0 0 0 0
Jump to Subroutine Conditionally
Example
Instruction Format
Effective Addressing Mode M M M R R R Mnemonic C C C C
Jsclr
Jump to Subroutine if Bit Clear
Condition Codes
Jsclr #n,Xea,xxxx Jsclr #n,Yea,xxxx
Jsclr #n,Xaa,xxxx Jsclr #n,Yaa,xxxx
Short Address aaaaaa Memory SpaceS Bit Number bbbbb
Jsclr #n,S,xxxx
Jsclr
Jset
Jump if Bit Set Operation Assembler Syntax
Jump if Bit Set
Jset #n,Xea,xxxx Jset #n,Yea,xxxx
Jump if Bit Set Instruction Format
Jset #n,Xpp,xxxx Jset #n,Ypp,xxxx
Jset #n,S,xxxx
Jump to Subroutine
JSR
Jump to Subroutine if Bit Set
Example
Jsset #n,Xea,xxxx Jsset #n,Yea,xxxx
Jsset #n,Xaa,xxxx Jsset #n,Yaa,xxxx
Jsset #n,Xpp,xxxx Jsset #n,Ypp,xxxx
Jsset #n,S,xxxx
Logical Shift Left
LSL D
Logical Shift Right
LSR D
Load Updated Address
Dest. Addr. Reg. D
Signed Multiply-Accumulate
PLY Mode
MAC X0,X0,A
Instruction Fields S1∗S2 Sign
Instruction Fields Sign
Sssss Constant
Signed Multiply-Accumulate and Round
Signed Multiply-Accumulate and Round Macr
Macr -Y0 #10, B
±S,#n,D
Move Data
Move S,D
Condition Codes
Move
Move
No Parallel Data Move Operation Assembler Syntax
No Parallel Data Move Instruction Format Opcode
Immediate Short Data Move
Tinations are not allowed within the same instruction
ABS B #$18,R1 Take absolute value of B, #$18R1
#xx=8-bit Immediate Short Data=iiiiiiii
Sign Ext Zero
Register to Register Data Move
MACR-X0,Y0,A
Instruction Format Opcode
Instruction Fields Or D Sign Ext Zero
Address Register Update Operation Assembler Syntax
Address Register Update
R R R
Memory Data Move Operation Assembler Syntax
Memory Data Move Example
Memory Data Move Instruction Format
Effective Register W Addressing Mode
M R R
Memory Data Move Sign Ext Zero
Register W Absolute Short Address a a a a a a
Instruction Descriptions
Xea D1 S2 D2 Xea,D1
Memory and Register Data Move
Class I Example
Memory and Register Data Move Class II Example
Class I Instruction Format
Memory and Register Data Move Condition Codes
R R
Memory and Register Data Move S1,D1 Sign Ext Zero
Memory and Register Data Move Class II Instruction Format
Sign Ext Zero Move Opcode
Memory Data Move Operation Assembler Syntax
After Execution $00123456000000
Yea,D #xxxxxx,D
Memory Data Move Sign Ext Zero
Register W Absolute Short Address aaaaaa
Instruction Descriptions
Class
Addl B,A B,X1 YR6-N6,B 2∗A+B A, update X1,B and R6
Register and Y Memory Data Move
Register and Y Memory Data Move Class II Example
By R1 and postincrement R1 Move Y0 to B
S1,D1 Yea,D2 . . . . . S1,D1 S2,Yea S1,D1 #xxxxxx,D2
Register and Y Memory Data Move Instruction Fields
S1 d Sign Ext Zero S2,D2
Register and Y Memory Data Move Class II Instruction Format
Dest
Long Memory Data Move Operation Assembler Syntax
Long Memory Data Move
CMP Y0,B
Long Memory Data Move Instruction Format
0 0 L 0 L A a a
XY Memory Data Move Operation Assembler Syntax
XY Memory Data Move Example
Mpyr X1,Y0,A
XY Memory Data Move Instruction Format
Sign Ext Zero Addressing Mode R r
XY Memory Data Move Effective Register
Move Control Register
Movec
Movec LC,X0 move LC into
2316 158 0 0 0 1 0 1 W 1 M M M R R R 0 s 1 d d d d d
Memory Space s S1, D1 D d d
Movec Xaa,D1 Movec S1,Xaa Movec Yaa,D1 Movec S1,Yaa
Movec S1,D2 Movec S2,D1
Instruction Fields Register S1, D1 D d d
Memory Space s
S2, D2 e e e e e e Sign Ext Zero
#xx=8-bit Immediate Short Data=i i i i i i i
Move Program Memory
Movem
Movem PR5+N5, LC
Movem S,Pea Movem Pea,D
D d d d Sign Ext Zero
Movem S,Paa Movem Paa,D
Movep
Movep
$FFFE BCR
Move Peripheral Data
Instruction Format X or Y Reference
Peripheral Space
Effective Memory Space Addressing Mode
Peripheral
Effective Peripheral Space S Addressing Mode
Instruction Format P Reference
Instruction Format Register Reference
Peripheral Space S Peripheral W
MPY MPY
Signed Multiply Operation
Signed Multiply
Signed Multiply Instruction Fields S1∗S2
Signed Multiply Instruction Format
Instruction Fields Sign Sssss constant
Signed Multiply and Round
Instruction SET Descriptions
Instruction Fields S1∗S2 Q Q Q Sign k
Mpyr ±S,#n,D
Negate Accumulator
NEG D
No Operation
PC+1PC NOP
None Timing 2 oscillator clock cycles Memory 1 program word
Normalize Accumulator Iteration
Norm R3,A
Normalize Accumulator Iteration Norm
Logical Complement
Not D
Logical Inclusive or Operation Assembler Syntax
Logical Inclusive or
Or Immediate with Control Register
Condition codes are not affected using these operands
Temp LC
Repeat Next Instruction
Temp LC LC Temp S LC REP
Immediately after REP
Jclr RTI JMP RTS Jset Stop
Jsclr Wait JSR Enddo
REP MAC X1,Y1,A
Condition Codes
REP Xea REP Yea
Absolute Short Address aaaaaa Memory Space s
Immediate Short Data hhhh i i i i i i i i
REP S
Instruction Fields D d d d
Dition Code Computation
Reset On-Chip Peripheral Devices
None Timing 4 oscillator clock cycles Memory 1 program word
Round Accumulator
RND a #$123456,X1 B,Y1
Condition Codes
RND D
Rotate Left
Opcode
Rotate Right
ROR D
Return from Interrupt
Opcode Instruction Fields
Return from Subroutine
Opcode
Subtract Long with Carry
SBC
Condition Codes
SBC S,D
Stop Instruction Processing
Restrictions
Subtract
SUB S,D
Shift Left and Subtract Accumulators
Shift Left and Subtract Accumulators Subl Condition Codes
Subl S,D
Shift Right and Subtract Accumulators
Shift Right and Subtract Accumulators Subr Condition Codes
Subr S,D
Operation Assembler Syntax Begin SWI exception processing
Software Interrupt
SWI
Opcode Instruction Fields
Transfer Conditionally
Cc’’ Mnemonic Condition
CMP X0,A
S1,D1 Mnemonic
C C
J D
Transfer Data ALU Register
TFR S,D
Test Accumulator
TST S
Wait for Interrupt
Condition Codes
Appendix B Benchmark Programs
Motorola Benchmark Programs
Section B.1 Introduction Section B.2 Benchmark Programs
Benchmark Programs Motorola
Introduction
Table B-1 27-MHz Benchmark Results for the DSP56001R27
Cycles
Benchmark Programs Motorola
Figure B-1 20-Tap FIR Filter Example Sheet 1
Benchmark Programs Motorola
Figure B-1 20-Tap FIR Filter Example Sheet 2
Benchmark Programs Motorola
Figure B-2 Radix 2, In-Place, Decimation-In-Time FFT Sheet 1
Benchmark Programs Motorola
Benchmark Programs
Motorola Benchmark Programs
+ yn 1wn-1 Ai1 bi1
Benchmark Programs
Benchmark Programs
Benchmark Programs
$FFC0
Figure B-5
Benchmark Programs
Benchmark Programs
Benchmark Programs
Benchmark Programs
Benchmark Programs
128 3846 256 8656 512 19296
Benchmark Programs
DSP56100 Family Manual Trouble Report
DSP56100 Family Manual Trouble Report
Index
Index
Index
Index
Index
AGU -6 data ALU -19 program control unit -8 summary -17 Pvcc
Zero Bit -10, A-17